
【题目】已知函数![]()
![]() ,g(x)=x2﹣1.
,g(x)=x2﹣1.
(1)求f(x)在点(0,f(0))处的切线方程.
(2)若h(x)=f(x)+g(x)有两个极值点x1,x2(x1<x2),求证:x1f(x1)>x2f(x2).
【答案】(1)y=﹣ax;(2)见解析
【解析】
![]() 对函数
对函数![]()
![]() 进行求导
进行求导![]() ,利用导数的几何意义求出
,利用导数的几何意义求出![]() 即为所求切线的斜率,代入点斜式求解即可;
即为所求切线的斜率,代入点斜式求解即可;
![]() 对函数
对函数![]() 求导,根据题意知,
求导,根据题意知,![]() 为方程
为方程![]() 的两个不同的实根,利用判别式
的两个不同的实根,利用判别式![]() 求出
求出![]() 的取值范围,再利用韦达定理判断出
的取值范围,再利用韦达定理判断出![]() 的范围, 要证明x1f(x1)>x2f(x2),即证明
的范围, 要证明x1f(x1)>x2f(x2),即证明![]() ,根据题意分别求出
,根据题意分别求出![]() 的表达式,然后作差,结合韦达定理把
的表达式,然后作差,结合韦达定理把![]() 用
用![]() 代换,构造函数m(x)=2x﹣1+2(1﹣x)lnx﹣2xln(1﹣x),x
代换,构造函数m(x)=2x﹣1+2(1﹣x)lnx﹣2xln(1﹣x),x![]() ,通过求导判断其单调性和最值,证明
,通过求导判断其单调性和最值,证明![]() 在
在![]() 上恒成立即可.
上恒成立即可.
(1)由题意知,![]() ,f(0)=0,
,f(0)=0,![]() ,
,
故f(x)在(0,f(0))处的切线方程y=﹣ax;
(2)由题意可知,h(x)=aln(1﹣x)+x2﹣1,x<1,
所以![]() 0在
0在![]() 上有2个不同的实数根,
上有2个不同的实数根,
即方程﹣2x2+2x﹣a=0在![]() 上有2个不同实根x1,x2,
上有2个不同实根x1,x2,
所以△=4﹣8a>0,即0<a![]() ,
,
由韦达定理可得,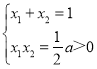 ,∴
,∴![]() ,
,
所以要证明x1f(x1)>x2f(x2),即证明![]() ,
,
∵![]() ,
,
因为![]() ,
,
所以![]()
=2x1ln(1﹣x1)﹣(1+x1),
同理![]() 2x2ln(1﹣x2)﹣(1+x2),
2x2ln(1﹣x2)﹣(1+x2),
所以![]() 2x1ln(1﹣x1)﹣(1+x1)﹣2x2ln(1﹣x2)+(1+x2)
2x1ln(1﹣x1)﹣(1+x1)﹣2x2ln(1﹣x2)+(1+x2)
=2x1ln(1﹣x1)﹣2x2ln(1﹣x2)+x2﹣x1,
因为![]() ,所以
,所以![]()
令m(x)=2x﹣1+2(1﹣x)lnx﹣2xln(1﹣x),x![]() ,
,
∴![]() 2[ln(1﹣x)
2[ln(1﹣x)![]() ]
]
![]() 0在(
0在(![]() )上恒成立,
)上恒成立,
故函数m(x)在(![]() )上单调递增,m(x)>m(
)上单调递增,m(x)>m(![]() )=0,
)=0,
故![]() 0,
0,
即x1f(x1)>x2f(x2).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分别五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意),其统计结果如下表(住宿满意度为x,餐饮满意度为y).
餐饮满意度y 人数 住宿满意度x | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 2 | 1 | 0 |
2 | 2 | 1 | 3 | 2 | 1 |
3 | 1 | 2 | 5 | 3 | 4 |
4 | 0 | 3 | 5 | 4 | 3 |
5 | 0 | 0 | 1 | 2 | 3 |
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义R在上的函数![]() 为奇函数,并且其图象关于x=1对称;当x∈(0,1]时,f(x)=9x﹣3.若数列{an}满足an=f(log2(64+n))(n∈N+);若n≤50时,当Sn=a1+a2+…+an取的最大值时,n=_____.
为奇函数,并且其图象关于x=1对称;当x∈(0,1]时,f(x)=9x﹣3.若数列{an}满足an=f(log2(64+n))(n∈N+);若n≤50时,当Sn=a1+a2+…+an取的最大值时,n=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批 5G 手机芯片进行测评,该公司随机调查了 100 颗芯片,所调查的芯片得分均在7,19内,将所得统计数据分为如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 六个小组,得到如图所示的频率分布直方图,其中
六个小组,得到如图所示的频率分布直方图,其中![]() .
.
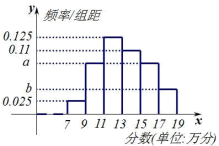
(1)求这 100 颗芯片评测分数的平均数;
(2)芯片公司另选 100 颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在 3 个工程手机中进行初测若 3 个工程手机的评分都达到 13 万分,则认定该芯片合格;若 3 个工程手机中只要有 2 个评分没达到 13 万分,则认定该芯片不合格;若 3 个工程手机中仅 1 个评分没有达到 13万分,则将该芯片再分别置于另外 2 个工程手机中进行二测,二测时,2 个工程手机的评分都达到 13万分,则认定该芯片合格;2个工程手机中只要有 1 个评分没达到 13 万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为 160 元,每颗芯片若被认定为合格或不合格,将不再进行后续测试.现手机公司测试部门预算的测试经费为 5 万元,试问预算经费是否足够测试完这 100 颗芯片?请说明理由.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的短轴长为
的短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .当
.当![]() 与
与![]() 连线的斜率为
连线的斜率为![]() 时,直线
时,直线![]() 的倾斜角为
的倾斜角为![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是以
是以![]() 为直径的圆上的任意一点,求证:
为直径的圆上的任意一点,求证:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com