【题目】将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为（ ）
A.
B.2+ 
C.4+
D.
【答案】C
【解析】解：由题意知，底面放三个钢球，上再落一个钢球时体积最小． 于是把钢球的球心连接，则又可得到一个棱长为2的小正四面体，则不难求出这个小正四面体的高为 
，
且由正四面体的性质可知：正四面体的中心到底面的距离是高的 
，且小正四面体的中心和正四面体容器的中心应该是重合的，
∴小正四面体的中心到底面的距离是 × = 
，正四面体的中心到底面的距离是 +1 （1即小钢球的半径），
所以可知正四棱锥的高的最小值为 （ +1）×4=4+ ，
故选 C．
【考点精析】掌握棱锥的结构特征是解答本题的根本，需要知道侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．
科目：高中数学 来源： 题型：
【题目】已知圆C：x2+y2﹣4x﹣4y+4=0，点E（3，4）．
（1）过点E的直线l与圆交与A，B两点，若AB=2 
，求直线l的方程；
（2）从圆C外一点P（x1 ， y1）向该圆引一条切线，切点记为M，O为坐标原点，且满足PM=PO，求使得PM取得最小值时点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，有一壁画，最高点A处离地面AO=4m，最低点B处离地面BO=2m，观赏它的C点在过墙角O点与地面成30°角的射线上． 
（1）设点C到墙的距离为x，当x= 
m时，求tanθ的值；
（2）问C点离墙多远时，视角θ最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥CD，∠ABC=90°，且CD=2，AB=BC=PA=1，PD= 
． 
（1）求三棱锥A﹣PCD的体积；
（2）问：棱PB上是否存在点E，使得PD∥平面ACE？若存在，求出 
的值，并加以证明；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在正方体ABCD﹣A1B1C1D1中，点M是平面A1B1C1D1内一点，且BM∥平面ACD1 ， 则tan∠DMD1的最大值为（ ） 
A.
B.1
C.2
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一个几何体的三视图如图所示．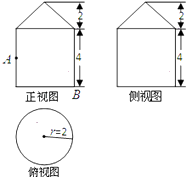 
（1）求此几何体的表面积；
（2）在如图的正视图中，如果点A为所在线段中点，点B为顶点，求在几何体侧面上从点A到点B的最短路径的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若正项数列{an}满足： 
=an+1﹣an（a∈N*），则称此数列为“比差等数列”．
（1）请写出一个“比差等数列”的前3项的值；
（2）设数列{an}是一个“比差等数列”
（i）求证：a2≥4；
（ii）记数列{an}的前n项和为Sn ， 求证：对于任意n∈N*，都有Sn＞ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱锥A﹣BCD的各个棱长都相等，E，F分别是棱AB，CD的中点，则EF与BC所成的角是（ ）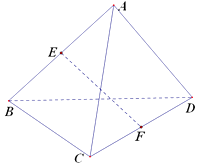 
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
