
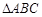 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,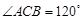 ,现将
,现将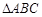 沿CD翻折成直二面角A-DC-B.(如图(2))
沿CD翻折成直二面角A-DC-B.(如图(2))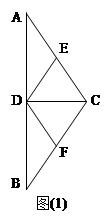
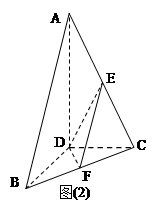
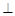 DE?证明你的结论.
DE?证明你的结论.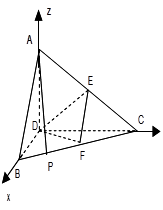
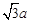 则A(0,0,
则A(0,0,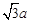 ),B(
),B(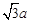 ,0,0), C(0,
,0,0), C(0,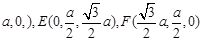 .……………………… 5分
.……………………… 5分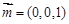 设平面EDF的法向量为
设平面EDF的法向量为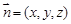 ,
,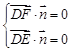 得
得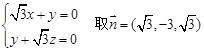 ,…………6分
,…………6分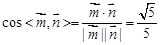 ,……………………………………… 7分
,……………………………………… 7分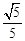 ;…………………………… 8分
;…………………………… 8分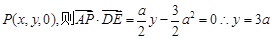 ,
,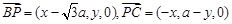 , ……………………………………… 9分
, ……………………………………… 9分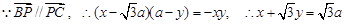 ………………………11分
………………………11分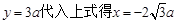 ,可知点P在BC的延长线上
,可知点P在BC的延长线上

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:不详 题型:解答题
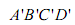 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.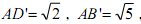 ,正方形的边长为
,正方形的边长为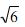 ,
, 的余弦值.
的余弦值.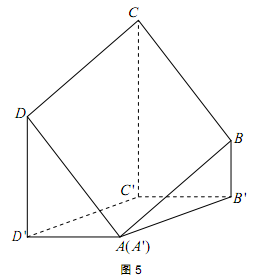
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
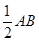 ,∠ACF=∠ADC=
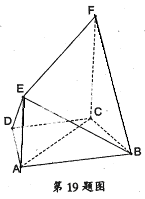
,∠ACF=∠ADC=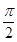 。
。
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
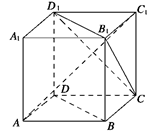
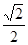 ;
;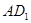 与BD为异面直线。
与BD为异面直线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com