
若圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,设圆心
相切,设圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 、
、![]() 为曲线
为曲线![]() 上的两点,点
上的两点,点![]() ,且满足
,且满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,过
,过![]() 、
、![]() 两点的圆
两点的圆![]() 与抛物线在点
与抛物线在点![]() 处有共同的切线,求圆
处有共同的切线,求圆![]() 的方程;
的方程;
(3)分别过![]() 、
、![]() 作曲线
作曲线![]() 的切线,两条切线交于点
的切线,两条切线交于点![]() ,若点
,若点![]() 恰好在直线
恰好在直线![]() 上,求证:
上,求证:![]() 与
与![]() 均为定值.
均为定值.
21.解:(1)依题意,点![]() 到定点
到定点![]() 的距离等于到定直线
的距离等于到定直线![]() 的距离,所以点
的距离,所以点![]() 的轨迹为抛物线,曲线
的轨迹为抛物线,曲线![]() 的方程为
的方程为![]() ; …………………………………………………………3分
; …………………………………………………………3分
(2)直线![]() 的方程是
的方程是![]() ,即
,即![]() ,
,
由![]() 得点
得点![]() 、
、![]() 的坐标是
的坐标是![]() 或
或![]() ,………………………………5分
,………………………………5分
当![]() 、
、![]() 时,由
时,由![]() 得
得![]() ,
,![]() ,
,
所以抛物线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() …………①
…………①
线段![]() 的中点坐标为
的中点坐标为![]() ,中垂线方程为
,中垂线方程为![]() ,即
,即![]() …………②
…………②
由①、②解得![]() , …………………………………………………………7分
, …………………………………………………………7分
于是,圆![]() 的方程为
的方程为![]() ,
,
即 ![]() , ………………………………………………………8分
, ………………………………………………………8分
当![]() 、
、![]() 时,抛物线
时,抛物线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,此时切线与
,此时切线与![]() 垂直,所求圆为以
垂直,所求圆为以![]() 为直径的圆,可求得圆为
为直径的圆,可求得圆为![]() , ……9分
, ……9分
(3)设![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的切线方程为
的切线方程为![]() ,
,
即![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,
,![]() ,……10分
,……10分
又 =
=![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() ,亦即
,亦即![]() ,所以
,所以![]() ,………………………………………11分
,………………………………………11分
而![]() ,
,![]() ,所以
,所以
![]()
![]()
![]() . …………………………………13分
. …………………………………13分


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(四) 题型:解答题
若圆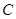 过点
过点 且与直线
且与直线 相切,设圆心
相切,设圆心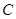 的轨迹为曲线
的轨迹为曲线 ,
,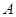 、
、 为曲线
为曲线 上的两点,点
上的两点,点 ,且满足
,且满足 .
.
(1)求曲线 的方程;
的方程;
(2)若 ,直线
,直线 的斜率为
的斜率为 ,过
,过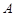 、
、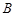 两点的圆
两点的圆 与抛物线在点
与抛物线在点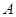 处有共同的切线,求圆
处有共同的切线,求圆 的方程;
的方程;
(3)分别过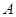 、
、 作曲线
作曲线 的切线,两条切线交于点
的切线,两条切线交于点 ,若点
,若点 恰好在直线
恰好在直线 上,求证:
上,求证: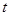 与
与 均为定值.
均为定值.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学文史类模拟试卷(三) 题型:解答题
已知动圆P过点 且与直线
且与直线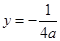 相切.
相切.
(Ⅰ) 求动圆圆心P的轨迹E的方程;
(Ⅱ) 设直线 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N.
① 证明:轨迹E点N处的切线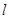 与AB平行;
与AB平行;
② 是否存在实数 ,使
,使 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 且与直线
且与直线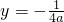 相切.
相切.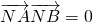 ?若存在,求a的值;若不存在,说明理由.
?若存在,求a的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)若圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,设圆心
相切,设圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 、
、![]() 为曲线
为曲线![]() 上的两点,点
上的两点,点![]() ,且满足
,且满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,过
,过![]() 、
、![]() 两点的圆
两点的圆![]() 与抛物线在点
与抛物线在点![]() 处有共同的切线,求圆
处有共同的切线,求圆![]() 的方程;
的方程;
(3)分别过![]() 、
、![]() 作曲线
作曲线![]() 的切线,两条切线交于点
的切线,两条切线交于点![]() ,若点
,若点![]() 恰好在直线
恰好在直线![]() 上,求证:
上,求证:![]() 与
与![]() 均为定值.
均为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com