
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明:AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(Ⅰ)由题意可知![]() ,设
,设![]() 且
且![]() ,求出点
,求出点![]() 的坐标,求出
的坐标,求出![]() 方程,得到
方程,得到![]() ,进而写出直线
,进而写出直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() 利用
利用 ![]() ,即可证明
,即可证明![]() ;
;
(Ⅱ)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,利用
,利用![]() 的面积是
的面积是![]() 的面积的两倍,求出
的面积的两倍,求出![]() 的坐标,由kAB=kDE可得
的坐标,由kAB=kDE可得![]() =
=![]() (x≠1).讨论即可得到
(x≠1).讨论即可得到![]() 中点的轨迹方程.
中点的轨迹方程.
试题解析:
(1)证明 由题意可知F![]() ,
,
设l1:y=a,l2:y=b,且ab≠0,A![]() ,B
,B![]() ,P
,P![]() ,Q
,Q![]() ,
,
R![]() .记过A,B两点的直线为l,
.记过A,B两点的直线为l,
则l的方程为2x-(a+b)y+ab=0.
因为点F在线段AB上,所以ab+1=0,
记直线AR的斜率为k1,直线FQ的斜率为k2,
所以k1=![]() ,k2=
,k2=![]() =-b,
=-b,
又因为ab+1=0,
所以k1=![]() =
=![]() =
=![]() =
=![]() =-b,
=-b,
所以k1=k2,即AR∥FQ.
(2)解 设直线AB与x轴的交点为D(x1,0),
所以S△ABF=![]() |a-b|FD=
|a-b|FD=![]() |a-b|
|a-b|![]() ,
,
又S△PQF=![]() ,所以由题意可得S△PQF=2S△ABF
,所以由题意可得S△PQF=2S△ABF
即:![]() =2×
=2×![]() ×|a-b|·
×|a-b|·![]() ,
,
解得x1=0(舍)或x1=1.
设满足条件的AB的中点为E(x,y).
当AB与x轴不垂直时,
由kAB=kDE可得![]() =
=![]() (x≠1).
(x≠1).
又![]() =
=![]() ,所以y2=x-1(x≠1).
,所以y2=x-1(x≠1).
当AB与x轴垂直时,E与D重合,
所以,所求轨迹方程为y2=x-1.


科目:高中数学 来源: 题型:
【题目】已知椭圆的左焦点为![]() ,有一质点A从
,有一质点A从![]() 处以速度v开始沿直线运动,经椭圆内壁反射
处以速度v开始沿直线运动,经椭圆内壁反射![]() 无论经过几次反射速率始终保持不变
无论经过几次反射速率始终保持不变![]() ,若质点第一次回到
,若质点第一次回到![]() 时,它所用的最长时间是最短时间的7倍,则椭圆的离心率e为
时,它所用的最长时间是最短时间的7倍,则椭圆的离心率e为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
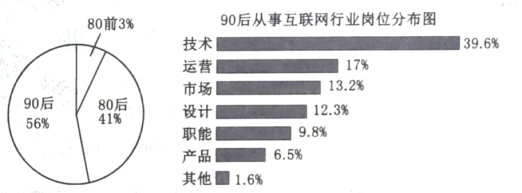
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为函数![]() (
(![]()
![]()
![]() )图象的一部分.
)图象的一部分.

(1)求函数![]() 的解析式,并写出
的解析式,并写出![]() 的振幅、周期、初相.
的振幅、周期、初相.
(2)求使得![]() 的x的集合.
的x的集合.
(3)两数![]() 的图象可由两数
的图象可由两数![]() 的图象经过怎样的变换而得到?
的图象经过怎样的变换而得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷是德国著名数学家,函数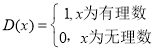 ,被称为狄利克雷函数,下面给出关于狄利克雷函数
,被称为狄利克雷函数,下面给出关于狄利克雷函数![]() 的五个结论:
的五个结论:
①若![]() 是无理数,则
是无理数,则![]() ;
;
②函数![]() 的值域是
的值域是![]() ;
;
③函数![]() 是偶函数;
是偶函数;
④若![]() 且
且![]() 为有理数,则
为有理数,则![]() 对任意的
对任意的![]() 恒成立;
恒成立;
⑤存在不同的三个点![]() ,使得
,使得![]() 为等边三角形.
为等边三角形.
其中正确结论的序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果存在函数
,如果存在函数![]() (
(![]() 为常数),使得
为常数),使得![]() 对一切实数
对一切实数![]() 都成立,则称
都成立,则称![]() 为函数
为函数![]() 的一个承托函数.给出如下命题:
的一个承托函数.给出如下命题:
① 函数![]() 是函数
是函数![]() 的一个承托函数;
的一个承托函数;
② 函数![]() 是函数
是函数![]() 的一个承托函数;
的一个承托函数;
③ 若函数![]() 是函数
是函数![]() 的一个承托函数,则
的一个承托函数,则![]() 的取值范围是
的取值范围是![]() ;
;
④ 值域是![]() 的函数
的函数![]() 不存在承托函数。 其中,所有正确命题的序号是__.
不存在承托函数。 其中,所有正确命题的序号是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com