
【题目】已知函数![]() ,则下述结论中错误的是( )
,则下述结论中错误的是( )
A.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 有且仅有
有且仅有![]() 个极小值点
个极小值点
B.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 上单调递增
上单调递增
C.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 的范围是
的范围是![]()
D.若![]() 图像关于
图像关于![]() 对称,且在
对称,且在![]() 单调,则
单调,则![]() 的最大值为
的最大值为![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
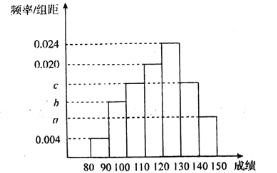
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的
和唯众传媒联合制作的![]() 开讲啦
开讲啦![]() 是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的
是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为
列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为![]() .
.
非常满意 | 满意 | 合计 | |
A | 30 | 15 | |
B | |||
合计 |
![]() 完成上述表格并根据表格判断是否有
完成上述表格并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
![]() 若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
|
|
|
|
|
|
|
|
附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com