
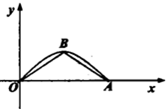
 如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )
如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 根据几何概率的求法:点P落在△ABO内的概率就是△ABO的面积与f(x)的图象与x轴所围成的区域的面积的比值.
解答 解:S△ABO=$\frac{1}{2}×π×1$=$\frac{π}{2}$,
设f(x)的图象与x轴所围成的区域为S,则S=${∫}_{0}^{π}sinxdx$=(-cosx)${|}_{0}^{π}$=2,
∴点P落在△OAB内的概率为P=$\frac{π}{4}$,
故选:A.
点评 本题主要考查三角函数、定积分、几何概型.首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A),然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.65<log0.65<50.6 | B. | 0.65<50.6<log0.65 | ||
| C. | log0.65<0.65<50.6 | D. | log0.65<50.6<0.65 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com