
【题目】如图,已知动直线l过点 ![]() ,且与圆O:x2+y2=1交于A、B两点.
,且与圆O:x2+y2=1交于A、B两点. 
(1)若直线l的斜率为 ![]() ,求△OAB的面积;
,求△OAB的面积;
(2)若直线l的斜率为0,点C是圆O上任意一点,求CA2+CB2的取值范围;
(3)是否存在一个定点Q(不同于点P),对于任意不与y轴重合的直线l,都有PQ平分∠AQB,若存在,求出定点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:因为直线l的斜率为 ![]() ,所以直线l
,所以直线l ![]() ,
,
则点O到直线l的距离 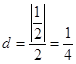 ,
,
所以弦AB的长度 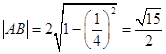 ,
,
所以 ![]()
(2)解:因为直线l的斜率为0,所以可知 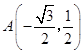 、
、 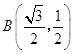 ,
,
设点C(x,y),则x2+y2=1,
又 ![]() ,所以CA2+CB2=4﹣2y,又y∈[﹣1,1],
,所以CA2+CB2=4﹣2y,又y∈[﹣1,1],
所以CA2+CB2的取值范围是[2,6]
(3)解:法一:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1,y1)、B(x2,y2),
因直线l不与y轴重合,设直线l ![]() ,
,
代入圆O得 ![]() ,
,
所以 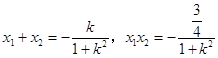 (*)
(*)
若PQ平分∠AQB,则根据角平分线的定义,AQ与BQ的斜率互为相反数
有 ![]() ,又
,又 ![]() ,
, ![]() ,
,
化简可得 ![]() ,
,
代入(*)式得 ![]() ,因为直线l任意,故
,因为直线l任意,故 ![]() ,
,
即t=2,即Q(0,2)
解法二:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1,y1)、B(x2,y2),
因直线l不与y轴重合,设直线l ![]() ,
,
代入圆O得 ![]() ,
,
所以 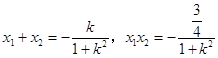 (*)
(*)
若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1,点B到y轴的距离d2满足 ![]() ,即
,即 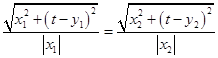 ,
,
化简可得 ![]() ,
,
代入(*)式得 ![]() ,因为直线l任意,故
,因为直线l任意,故 ![]() ,
,
即t=2,即Q(0,2)
【解析】(1)因为直线l的斜率为 ![]() ,所以直线l
,所以直线l ![]() ,利用弦长、半径、弦心距的关系,求得弦长及△OAB的高,即可求出面积.(2)因为直线l的斜率为0,所以可知
,利用弦长、半径、弦心距的关系,求得弦长及△OAB的高,即可求出面积.(2)因为直线l的斜率为0,所以可知 ![]() 、
、 ![]() ,设点C(x,y),则x2+y2=1,又
,设点C(x,y),则x2+y2=1,又 ![]() =4﹣2y,又y∈[﹣1,1],
=4﹣2y,又y∈[﹣1,1],
即可得CA2+CB2的取值范围.(3)法一:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1,y1)、B(x2,y2),因直线l不与y轴重合,设直线l ![]() ,代入圆O得
,代入圆O得 ![]() ,所以
,所以 ![]() (*) 由AQ与BQ的斜率互为相反数,可得
(*) 由AQ与BQ的斜率互为相反数,可得 ![]() ,即求得t;解法二:若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1,点B到y轴的距离d2满足
,即求得t;解法二:若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1,点B到y轴的距离d2满足 ![]() ,即
,即 ![]() ,化简可得
,化简可得 ![]() ,同时求得t.
,同时求得t.
【考点精析】解答此题的关键在于理解直线与圆的三种位置关系的相关知识,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的上顶点M与左、右焦点F1、F2构成三角形MF1F2面积为
的上顶点M与左、右焦点F1、F2构成三角形MF1F2面积为 ![]() ,又椭圆C的离心率为
,又椭圆C的离心率为 ![]() .
.
(1)求椭圆C的方程;
(2)椭圆C的下顶点为N,过点T(t,2)(t≠0)的直线TM,TN分别与椭圆C交于E,F两点.若△TMN的面积是△TEF的面积的k倍,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(1)设bn= ![]() ﹣1,证明:数列{bn}是等比数列,并求数列{an}的通项公式an;
﹣1,证明:数列{bn}是等比数列,并求数列{an}的通项公式an;
(2)记数列{nbn}的前n项和为Tn , 求证:Tn<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>5,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=7,b=14,A=30°
B.b=4,c=5,B=30°
C.b=25,c=3,C=150°
D.a= ![]() ,b=
,b= ![]() ,B=60°
,B=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°。 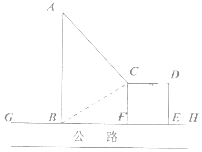
(1)求y关于x的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:x取何值时,该公司建设中转站围墙和两条道路总造价M最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com