[题目]将一颗骰子先后抛掷2次.观察向上的点数.求:(1)两数之和为5的概率,(2)两数中至少有一个奇数的概率．题目和参考答案——青夏教育精英家教网—

【题目】将一颗骰子先后抛掷2次，观察向上的点数，求：

(1)两数之和为5的概率；

(2)两数中至少有一个奇数的概率．

【答案】（1）；（2）

【解析】

试题分析：（Ⅰ）通过列举可发现此问题中含有36个基本事件，而两数之和为5的有（1,4）、（4,1）、（2.3）、（3、2）4种，利用古典概型概率计算公式可得概率为；（Ⅱ）求出对立面的概率：对立面含的基本事件为（2，2）、（4,4）、（6,6）、（2,4）、（4,2）、（2，6）、（6,2）、（4,6）、（6、4）共9种，所以所求的概率为.

试题解析：将一颗骰子先后抛掷2次，此问题中含有36个等可能基本事件．

(Ⅰ)记“两数之和为5”为事件A，则事件A中含有4个基本事件，所以

P(A)＝＝.

答：两数之和为5的概率为. 6分

(Ⅱ)记“两数中至少有一个为奇数”为事件B，则事件B与“两数均为偶数”为对立事件，所以P(B)＝1－＝.

答：两数中至少有一个为奇数的概率为. 12分

练习册系列答案

PASS教材搭档系列答案

天利38套中考总复习命题规律与必考压轴题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，四面体ABCD中，AB、BC、BD两两垂直，AB=BC=BD=4，E、F分别为棱BC、AD的中点．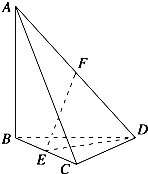

（1）求异面直线AB与EF所成角的余弦值；
（2）求E到平面ACD的距离；
（3）求EF与平面ACD所成角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】经过对K2的统计量的研究，得到了若干个观测值，当K2≈6.706时，我们认为两分类变量A、B(　　)

A. 有67.06%的把握认为A与B有关系 B. 有99%的把握认为A与B有关系

C. 有0.010的把握认为A与B有关系 D. 没有充分理由说明A与B有关系

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学为提升学生的英语学习能力，进行了主题分别为“听”、“说”、“读”、“写”四场竞赛．规定：每场竞赛的前三名得分分别为，，（，且，，），选手的最终得分为各场得分之和．最终甲、乙、丙三人包揽了每场竞赛的前三名，在四场竞赛中，已知甲最终分为分，乙最终得分为分，丙最终得分为分，且乙在“听”这场竞赛中获得了第一名，则“听”这场竞赛的第三名是（）

A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某产品的广告费用x与销售额y的统计数据如下表：

广告费用x(万元)	4	2	3	5
销售额y(万元)	49	26	39	54

(1)求根据上表可得线性回归方程=x+；

(2) 模型预报广告费用为6万元时销售额为多少

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：

组　别	频数	频率
[145.5，149.5）	1	0.02
[149.5，153.5）	4	0.08
[153.5，157.5）	20	0.40
[157.5，161.5）	15	0.30
[161.5，165.5）	8	0.16
[165.5，169.5）	m	n
合　计	M	N