【题目】已知真命题：“函数
的图象关于点
成中心对称图形”的等价条件为“函数
是奇函数”.
（1）将函数
的图象向左平移1个单位，再向上平移2个单位，求此时图象对应的函数解析式，并利用题设中的真命题求函数
图象对称中心的坐标；
（2）已知命题：“函数的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b，使得函数是偶函数”.断该命题的真假.如果是真命题，请给予证明；如果是假命题，请说明理由，并类比题设的真命题对它进行修改，使之成为真命题（不必证明）.
科目：高中数学 来源： 题型：
【题目】榆林市政府坚持保护环境和节约资源，坚持推进生态文明建设。若市财政局下拨专款100百万元，分别用于植绿护绿和处理污染两个生态维护项目，植绿护绿项目五年内带来的生态收益可表示为投放资金
(单位：百万元)的函数
(单位：百万元)：
，处理污染项目五年内带来的生态收益可表示为投放资金单位：(单位：百万元)的函数
(单位：百万元)：
。
(1)设分配给植绿护绿项目的资金为(百万元)，则两个生态项目五年内带来的收益总和为y，写出y关于的函数解析式和定义域；
(2)试求出y的最大值，并求出此时对两个生态项目的投资分别为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用，服用药后每毫升血液中的含药量
（微克）与服药的时间
（小时）之间近似满足如图所示的曲线，其中
是线段，曲线
是函数
（
，
，且
，
是常数）的图象.
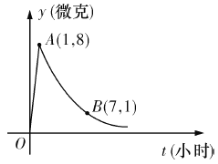
（1）写出服药后关于的函数关系式；
（2）据测定，每毫升血液中的含药量不少于
微克时治疗疾病有效.假设某人第一次服药为早上
，为保持疗效，第二次服药最迟应当在当天几点钟？
（3）若按（2）中的最迟时间服用第二次药，则第二次服药后
小时，该病人每毫升血液中的含药量为多少微克？（精确到
微克）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给定
，
，
，
所对的边分别是
，
，
，在所在平面作直线
与的某两边相交，沿将折成一个空间图形，将由分成的小三角形的不在上的顶点与另一部分的顶点连接，形成一个三棱锥或四棱锥。问：
（1）当
时，如何作，并折成何种锥体，才能使所得锥体体积最大？（需详证）
（2）当
时，如何作，并折成何种锥体，才能使所得锥体体积最大？（叙述结果，不要证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图.考虑以下结论：
①甲地该月14时的平均气温低于乙地该月14时的平均气温；
②甲地该月14时的平均气温高于乙地该月14时的平均气温；
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差；
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为（ ）
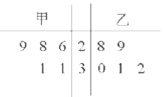
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
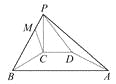
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
