
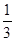 ,乙组能使生物成活的概率为
,乙组能使生物成活的概率为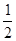 ,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.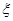 ,求
,求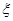 的期望.
的期望.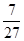 ;(2)
;(2)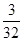 ;(3)
;(3)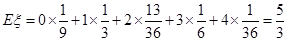 .
.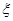 的所有可能取值,然后由相互独立事件的概率乘法公式计算出各种取值的概率,列出分布列,进而由公式
的所有可能取值,然后由相互独立事件的概率乘法公式计算出各种取值的概率,列出分布列,进而由公式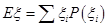 求出
求出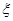 的数学期望即可.
的数学期望即可.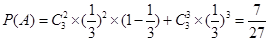 4分
4分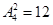 种,所以所求的概率为
种,所以所求的概率为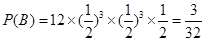 .
.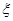 的取值为0,1,2,3,4
的取值为0,1,2,3,4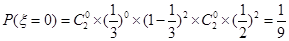
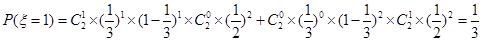
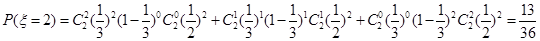
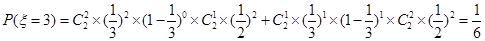
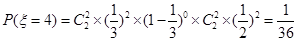 9分
9分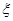 的分布列为
的分布列为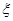 | 0 | 1 | 2 | 3 | 4 |
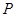 |  | 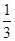 | 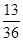 | 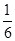 | 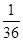 |
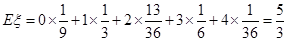 12分.
12分.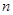 次独立重复试验某事件恰好发生
次独立重复试验某事件恰好发生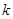 次的概率;2.相互独立事件的概率乘法公式;3.随机变量的期望.
次的概率;2.相互独立事件的概率乘法公式;3.随机变量的期望.

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.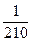 | B.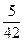 | C. | D.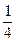 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
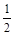 ,乙每次击中目标的概率为
,乙每次击中目标的概率为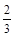
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 }为
}为 .如果
.如果 为数列{
为数列{ }的前
}的前 项和,那么
项和,那么 的概率为 ( )
的概率为 ( ) A. | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com