
【题目】为调查乘客的候车情况,公交公司在某为台的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,将他们的候车时间(单位:分钟)作为样本分成
人,将他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 候车时间 | 人数 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求这![]() 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这![]() 名候车乘客中候车时间少于
名候车乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的![]() 人中随机抽取
人中随机抽取![]() 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
【答案】(1)![]() 分钟;(2)
分钟;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)累积各组中与频数的积,可得这![]() 名乘客总和,即可利用公式求解平均的候车时间;(2)根据
名乘客总和,即可利用公式求解平均的候车时间;(2)根据![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的频数和为
分钟的频数和为![]() ,可估计这
,可估计这![]() 名乘客候车时间少于
名乘客候车时间少于![]() 分钟的人数;(3)将两组乘客编号,进而列举出所有基本事件和抽到的两人恰好来自于不同组的基本事件个数,代入古典概型的概率公式可得答案.
分钟的人数;(3)将两组乘客编号,进而列举出所有基本事件和抽到的两人恰好来自于不同组的基本事件个数,代入古典概型的概率公式可得答案.
试题解析:(1)由图表得:![]() ,
,
所以这![]() 名乘客的平均候车时间为
名乘客的平均候车时间为![]() 分钟.
分钟.
(2)由图表得:这![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的人数为
分钟的人数为![]() ,所以,这
,所以,这![]() 名乘客中候车时间少于
名乘客中候车时间少于![]() 分钟的人数大约等于
分钟的人数大约等于![]() .
.
(3)设第三组的乘客为![]() ,第四组的乘客
,第四组的乘客![]() ,
,![]() ,“抽到的的两人恰好来自不同的组”为事件
,“抽到的的两人恰好来自不同的组”为事件![]() .所得基本事件共有
.所得基本事件共有![]() 种,即
种,即![]()
![]() .
.
其中事件![]() 包含基本事件
包含基本事件![]() 种,,由古典概型可得
种,,由古典概型可得![]() ,即所求概率等于
,即所求概率等于![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象沿x轴向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若函数g(x)的图象关于y轴对称,则当φ取最小的值时,g(0)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列![]() 的前
的前![]() 项和为
项和为![]() ,首项
,首项![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记![]()
![]() ,是否存在正整数
,是否存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
,![]() 恒成立?若存在,求正整数
恒成立?若存在,求正整数![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证: 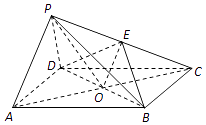
(1)直线PA∥平面BDE;
(2)平面BDE⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com