
分析 (1)利用直接法求动点P的轨迹方程;
(2)先表示出线段AB长度,再利用基本不等式,求出最小值.
解答 解 (1)设P(x,y),则
∵动点P到点F($\sqrt{2}$,0)的距离与它到直线x=2$\sqrt{2}$的距离之比为$\frac{{\sqrt{2}}}{2}$,
∴$\frac{\sqrt{(x-\sqrt{2})^{2}+{y}^{2}}}{|x-2\sqrt{2}|}$=$\frac{{\sqrt{2}}}{2}$,
化简可得动点P的轨迹方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1,
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0.
因为OA⊥OB,所以$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
即tx0+2y0=0,解得t=-$\frac{2{y}_{0}}{{x}_{0}}$.
又x02+2y02=4,
所以|AB|2=(x0-t)2+(y0-2)2
=(x0-t)2+(y0-2)2
=$\frac{{{x}_{0}}^{2}}{2}$+$\frac{8}{{{x}_{0}}^{2}}$+4(0<x02≤4).
因为$\frac{{{x}_{0}}^{2}}{2}$+$\frac{8}{{{x}_{0}}^{2}}$≥4(0<x02≤4),且当x02=4时等号成立,
所以|AB|2≥8.
故线段AB长度的最小值为2$\sqrt{2}$.
点评 本题考查轨迹方程,考查基本不等式的运用,考查学生的计算能力,属于中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
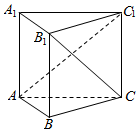 三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )
三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,长方体ABCD-A′B′C′D′中,AA′=3,AB=4,AD=5,E、F分别是线段AA′和AC的中点,则异面直线EF与CD′所成的角是( )
如图,长方体ABCD-A′B′C′D′中,AA′=3,AB=4,AD=5,E、F分别是线段AA′和AC的中点,则异面直线EF与CD′所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com