
(满分12分)已知a,b是实数,函数
 和
和 是
是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上单调性一致
上单调性一致
(1)设 ,若
,若 和
和 在区间
在区间 上单调性一致,求b的取值范围;
上单调性一致,求b的取值范围;
(2)设 且
且 ,若
,若 和
和 在以a,b为端点的开区间上单调性一致,
在以a,b为端点的开区间上单调性一致,
求|a―b|的最大值
科目:高中数学 来源: 题型:
(本小题满分12分)已知A(1,f′(1))是函数ks5uy=f(x)的导函数ks5u图像上的一点,点B的坐标为(x,㏑(x+1)),向量![]() =(1,1),设f(x)=
=(1,1),设f(x)=![]() ·
·![]()
(1)求函数ks5uy=f(x)的表达式;
(2)若x∈[-1,1]时,不等式![]() x
x![]() ≤f(x
≤f(x![]() )
)![]() +m
+m![]() -
-![]() m-3都恒成立,求实数ks5um 的取值范围.
m-3都恒成立,求实数ks5um 的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知A、B、C为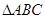 的三个内角且向量
的三个内角且向量
 共线。
共线。
(Ⅰ)求角C的大小:
(Ⅱ)设角 的对边分别是
的对边分别是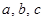 ,且满足
,且满足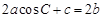 ,试判断
,试判断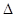
 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高考模拟系列文科数学试卷(二)(新课标版)(解析版) 题型:解答题
(本小题满分12分)已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(Ⅰ)若用数组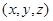 中的
中的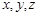 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组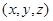 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届山东省高一上学期12月月考数学 题型:解答题
(本小题满分12分)已知a ,b
,b .
.
(1) 求a -2b;
(2) 设a, b的夹角为
 ,求
,求 的值;
的值;
(3)若向量a+kb与a-kb互相垂直,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com