分析:(Ⅰ)要证A1C⊥BF,只需证明BF垂直A1C在面BC1内的射影B1C即可;
(Ⅱ)连接AC交BD于O,则O为AC中点,连接OF,要证AC1∥平面BDF,只需证明AC1平行平面BDF内的直线OF即可,(利用数据计算出F为为C1C的中点);
(Ⅲ)说明∠FOC为二面角F-BD-C的平面角,解Rt△ABC求二面角F-BD-C的大小.
解答: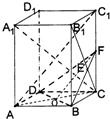
证明:(I)在长方体中,A
1B
1⊥面BC
1,
B
1C为A
1C在面BC
1内的射影,
BF?面BC
1,
且BF⊥B
1C,∴A
1C⊥BF.(3分)
证明(II)∵AB=BC=3,BB
1=3
,
在Rt△B
1BC中,B
1C=3
,∵BF⊥B
1C于E,∴BC
2=CE•CB
1,得CE=
,
由△BB
1E∽△FCE得
==,即F为C
1C的中点.(7分)
连接AC交BD于O,则O为AC中点,连接OF,则OF∥AC
1,∵AC
1?面BDF,OF?面BDF,∴AC
1∥平面BDF.(9分)
解(III)在长方体中,C
1C⊥面AC,OC为OF在面AC上的射影,BD?面AC,且BD⊥AC,∴BD⊥OF,
∴∠FOC为二面角F-BD-C的平面角.(11分)
在Rt△ABC中,OC=
AC=,CF=C1C=,∴OC=CF,∴∠FOC=45°
∴二面角F-BD-C的大小为45°(13分)
点评:本题考查直线与平面平行的判定,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.

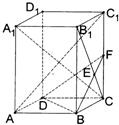 已知长方体ABCD-A1B1C1D1中,棱AB=BC=3,BB1=3
已知长方体ABCD-A1B1C1D1中,棱AB=BC=3,BB1=3 证明:(I)在长方体中,A1B1⊥面BC1,
证明:(I)在长方体中,A1B1⊥面BC1,

 天天向上口算本系列答案
天天向上口算本系列答案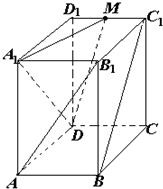 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.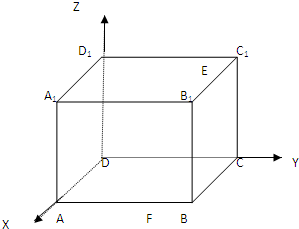 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=
已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=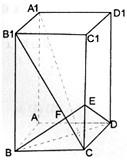 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.