
| A. | (0,1) | B. | [1,+∞) | C. | (1,2)∪(2,+∞) | D. | [1,2)∪(2,+∞) |
分析 利用直线y=k(x-1)恒过的定点在椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1内,计算即得结论.
解答 解:∵直线y=k(x-1)恒过定点P(1,0),
∴直线y=k(x-1)与椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1恒有公共点,
即点P(1,0)在椭圆内或椭圆上,
∴$\frac{1}{m}$≤1,即m≥1,
又m≠2,否则$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1是圆而非椭圆,
∴1≤m<2或m>2,
故选:D.
点评 本题考查直线与椭圆的位置关系,注意解题方法的积累,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:解答题
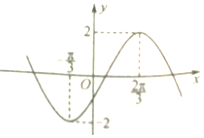 已知函数f(x)=Asin(ωx-$\frac{π}{6}$)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
已知函数f(x)=Asin(ωx-$\frac{π}{6}$)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q为真 | B. | p∨q为假 | C. | p∧(¬p)为真 | D. | (¬p)∨q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com