
【题目】某城市随机抽取一个月(30天)的空气质量指数API监测数据,统计结果如下:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | (300,350] |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 2 | 4 | 5 | 9 | 4 | 3 | 3 |
(Ⅰ)根据以上数据估计该城市这30天空气质量指数API的平均值;
(Ⅱ)若该城市某企业因空气污染每天造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系式为:
S= 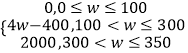
若在本月30天中随机抽取一天,试估计该天经济损失S大于200元且不超过600元的概率.
科目:高中数学 来源: 题型:
【题目】定义:分子为1且分母为正整数的分数称为单位分数.我们可以把1分拆为若干个不同的单位分数之和. 如:1= ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,…依此类推可得:1=
,…依此类推可得:1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,其中m≤n,m,n∈N* . 设1≤x≤m,1≤y≤n,则
,其中m≤n,m,n∈N* . 设1≤x≤m,1≤y≤n,则 ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)是定义在R上的奇函数,且在区间(﹣∞,0]上是减函数,则不等式f(lnx)<﹣f(1)的解集为( )
A.(e,+∞)
B.( ![]() ,+∞)
,+∞)
C.( ![]() ,e)
,e)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=Acos(ωx+φ)(其中A>0,ω>0,﹣ ![]() <φ<
<φ< ![]() )的图象如图所示,为得到的g(x)=Acosωx的图象,可以将f(x)的图象( )
)的图象如图所示,为得到的g(x)=Acosωx的图象,可以将f(x)的图象( ) 
A.向左平移 ![]()
B.向左平移 ![]()
C.向右平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,给出的是计算 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() 的值的程序框图,其中判断框内可填入的是( )
的值的程序框图,其中判断框内可填入的是( ) 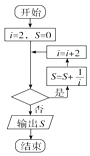
A.i≤2 021?
B.i≤2 019?
C.i≤2 017?
D.i≤2 015?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级的A,B,C三个班共有学生120人,为调查他们的体育锻炼情况,用分层抽样的方法从这三个班中分别抽取4,5,6名学生进行调查. (Ⅰ)求A,B,C三个班各有学生多少人;
(Ⅱ)记从C班抽取学生的编号依次为C1 , C2 , C3 , C4 , C5 , C6 , 现从这6名学生中随机抽取2名做进一步的数据分析.
(i)列出所有可能抽取的结果;
(ii)设A为事件“编号为C1和C2的2名学生中恰有一人被抽到”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( ) 
A.![]()
B.1﹣ ![]()
C.![]()
D.1﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括: 
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用文字和公式写出计算山顶M海拔高度的步骤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙M:(x+1)2+y2= ![]() 的圆心为M,⊙N:(x﹣1)2+y2=
的圆心为M,⊙N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)设A,B分别为曲线P与x轴的左右两个交点,过点(1,0)的直线l与曲线P交于C,D两点.若 ![]() =12,求直线l的方程.
=12,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com