
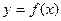 的定义域为R,对任意
的定义域为R,对任意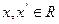 ,均有
,均有 ,且对任意
,且对任意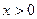 都有
都有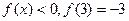 。
。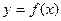 在R上是单调函数;
在R上是单调函数;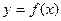 的奇偶性,并证明。
的奇偶性,并证明。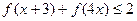 。
。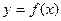 在
在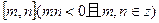 上的值域;
上的值域;

 ,令
,令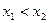


 ……………………………………………2分
……………………………………………2分
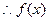 在R上是单调减函数 ……………………………………………4分
在R上是单调减函数 ……………………………………………4分 为奇函数,令
为奇函数,令 ,有
,有 …………………………5分
…………………………5分 ,有
,有
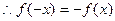 ………………………………………………7分
………………………………………………7分 ……………………………………………8分
……………………………………………8分

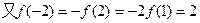 ………………………………………9分
………………………………………9分 原不等式为:
原不等式为: ……………………………………10分
……………………………………10分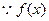 在R上递减,
在R上递减,
 不等式的解集为
不等式的解集为 …………………………………11分
…………………………………11分




 ………………………………………………………12分
………………………………………………………12分 为奇函数,
为奇函数, …………………13分
…………………13分 在
在 上递减,
上递减,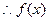 的值域为
的值域为 …………………………………………14分
…………………………………………14分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
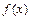 是定义在
是定义在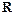 上的奇函数,当
上的奇函数,当 时,
时,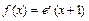 .给出以下命题:
.给出以下命题: ①当
①当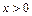 时,
时, ; ②函数
; ②函数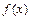 有3个零点;
有3个零点; 的解集为
的解集为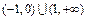 ; ④
; ④ ,都有
,都有 .
.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com