
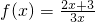 £¬ŹżĮŠ{an}¶Ōn”Ż2£¬n”ŹN×ÜÓŠ
£¬ŹżĮŠ{an}¶Ōn”Ż2£¬n”ŹN×ÜÓŠ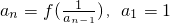 £»
£» µÄ×ÓŹżĮŠ£Ø¼“{bn}ÖŠµÄĆæŅ»Ļī¶¼ŹĒ
µÄ×ÓŹżĮŠ£Ø¼“{bn}ÖŠµÄĆæŅ»Ļī¶¼ŹĒ µÄĻī£¬ĒŅ°“ŌŚ
µÄĻī£¬ĒŅ°“ŌŚ ÖŠµÄĖ³ŠņÅÅĮŠ£©¢Ś{bn}ĪŖĪŽĒīµČ±ČŹżĮŠ£¬ĖüµÄø÷ĻīŗĶĪŖ
ÖŠµÄĖ³ŠņÅÅĮŠ£©¢Ś{bn}ĪŖĪŽĒīµČ±ČŹżĮŠ£¬ĖüµÄø÷ĻīŗĶĪŖ £®ÕāŃłµÄŹżĮŠŹĒ·ń“ęŌŚ£æČō“ęŌŚ£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄŹżĮŠ{bn}£¬Š“³öĖüµÄĶØĻī¹«Ź½£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
£®ÕāŃłµÄŹżĮŠŹĒ·ń“ęŌŚ£æČō“ęŌŚ£¬Ēó³öĖłÓŠ·ūŗĻĢõ¼žµÄŹżĮŠ{bn}£¬Š“³öĖüµÄĶØĻī¹«Ź½£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®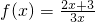 £¬ÓÖ
£¬ÓÖ £Ø2·Ö£©
£Ø2·Ö£© ĪŖ¹«²īµÄµČ²īŹżĮŠ£¬¼“
ĪŖ¹«²īµÄµČ²īŹżĮŠ£¬¼“ £Øn”ŹN*£©£Ø4·Ö£©
£Øn”ŹN*£©£Ø4·Ö£©
 £Ø6·Ö£©
£Ø6·Ö£© £Ø8·Ö£©
£Ø8·Ö£© £Ø10·Ö£©
£Ø10·Ö£© £¬¹«±Č
£¬¹«±Č £¬Ōņ
£¬Ōņ £Øk£¬p”ŹN*£©¶ŌČĪŅāµÄn”ŹN*¾ł³ÉĮ¢£¬¹ŹmŹĒÕżĘꏿ£¬ÓÖS“ęŌŚ£¬ĖłŅŌm£¾1£Ø12·Ö£©
£Øk£¬p”ŹN*£©¶ŌČĪŅāµÄn”ŹN*¾ł³ÉĮ¢£¬¹ŹmŹĒÕżĘꏿ£¬ÓÖS“ęŌŚ£¬ĖłŅŌm£¾1£Ø12·Ö£© £¬“ĖŹ±
£¬“ĖŹ± £¬
£¬ £¬³ÉĮ¢ £Ø13·Ö£©
£¬³ÉĮ¢ £Ø13·Ö£© £¬“ĖŹ±
£¬“ĖŹ± ¹Ź²»³ÉĮ¢ £Ø14·Ö£©
¹Ź²»³ÉĮ¢ £Ø14·Ö£© £¬“ĖŹ±
£¬“ĖŹ± £¬
£¬ £¬³ÉĮ¢ £Ø15·Ö£©
£¬³ÉĮ¢ £Ø15·Ö£© £¬ÓÉ
£¬ÓÉ £¬µĆ
£¬µĆ £¬Éč
£¬Éč £¬Ōņ
£¬Ōņ £¬ÓÖŅņĪŖk”ŹN*£¬ĖłŅŌk=1£¬2£¬“ĖŹ±b1=1»ņ
£¬ÓÖŅņĪŖk”ŹN*£¬ĖłŅŌk=1£¬2£¬“ĖŹ±b1=1»ņ ·Ö±š“śČė
·Ö±š“śČė £¬µĆµ½q£¼0²»ŗĻĢāŅā£Ø18·Ö£©
£¬µĆµ½q£¼0²»ŗĻĢāŅā£Ø18·Ö£© »ņ
»ņ £Ø20·Ö£©
£Ø20·Ö£© £¬¹«±Č
£¬¹«±Č £¬µĆµ½
£¬µĆµ½ £Øk£¬p”ŹN*£©¶ŌČĪŅāµÄn”ŹN*¾ł³ÉĮ¢£¬¹ŹmŹĒÕżĘꏿ£¬ÓÖS“ęŌŚ£¬ĖłŅŌm£¾1£»ŌŁ¶ŌmµÄȔֵ½ųŠŠĢÖĀŪ£¬¼“æɵƵ½ĖłÓŠ·ūŗĻĢõ¼žµÄŹżĮŠ{bn}£¬Š“³öĖüµÄĶØĻī¹«Ź½£®
£Øk£¬p”ŹN*£©¶ŌČĪŅāµÄn”ŹN*¾ł³ÉĮ¢£¬¹ŹmŹĒÕżĘꏿ£¬ÓÖS“ęŌŚ£¬ĖłŅŌm£¾1£»ŌŁ¶ŌmµÄȔֵ½ųŠŠĢÖĀŪ£¬¼“æɵƵ½ĖłÓŠ·ūŗĻĢõ¼žµÄŹżĮŠ{bn}£¬Š“³öĖüµÄĶØĻī¹«Ź½£®


| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| x |
| 1 |
| p(x) |
| 5 |
| x |
| 1 |
| 2 |
| x |
| 3 |
| x |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 |
| an |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
|
| 1 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 1 | f(n) |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com