
【题目】已知定点![]() ,
,![]() ,动点P为平面上一个动点,且直线SP,TP的斜率之积为
,动点P为平面上一个动点,且直线SP,TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在斜率为![]() 直线l,使得l交轨迹E于M,N两点,且
直线l,使得l交轨迹E于M,N两点,且![]() 恰是
恰是![]() 的重心?若存在,求l的方程;若不存在,说明理由.
的重心?若存在,求l的方程;若不存在,说明理由.
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】某品牌布娃娃做促销活动:已知有50个布娃娃,其中一些布娃娃里面有奖品,参与者可以先在50个布娃娃中购买5个,看完5个布娃娃里面的结果再决定是否将剩下的布娃娃全部购买,设每个布娃娃有奖品的概率为![]() ,且各个布娃娃是否有奖品相互独立.
,且各个布娃娃是否有奖品相互独立.
(1)记5个布娃娃中有1个有奖品的概率为![]() ,当
,当![]() 时,
时,![]() 的最大值,求
的最大值,求![]() ;
;
(2)假如这5个布娃娃中恰有1个有奖品,以上问中的![]() 作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
(3)若已知50件布娃娃中有10个布娃娃有奖品,从这堆布娃娃中任意购买5个,若抽到k个有奖品可能性最大,求k的值.(k为正整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6名选手参加才艺比赛,其中男、女选手各3名,且3名男选手分别表演歌唱、舞蹈和魔术,3名女选手分别表演歌唱、舞蹈和魔术,若要求相邻出场的选手性别不同且表演的节目不同,则不同的出场方式的种数为( )
A.6B.12C.18D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在定义域(0,+∞)上是单调函数,且x∈(0,+∞),f(f(x)﹣ex+x)=e.若不等式2f(x)﹣f′(x)﹣3≥ax对x∈(0,+∞)恒成立,则a的取值范围是( )
A.(﹣∞,e﹣2]B.(﹣∞,e﹣1]C.(﹣∞,2e﹣3]D.(﹣∞,2e﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,三角形
,三角形![]() 是等边三角形,平面
是等边三角形,平面![]() 平面
平面![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.
的中点.
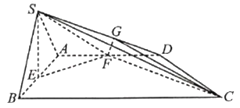
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处取得极大值或极小值,则称
处取得极大值或极小值,则称![]() 为函数
为函数![]() 的极值点.设函数
的极值点.设函数![]() .
.
(1)若函数![]() 在
在![]() 上无极值点,求
上无极值点,求![]() 的取值范围;
的取值范围;
(2)求证:对任意实数![]() ,在函数
,在函数![]() 的图象上总存在两条切线相互平行;
的图象上总存在两条切线相互平行;
(3)当![]() 时,若函数
时,若函数![]() 的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,抛物线E顶点在坐标原点,焦点为![]() .以坐标原点为极点,x轴非负半轴为极轴建立极坐标系.
.以坐标原点为极点,x轴非负半轴为极轴建立极坐标系.
(Ⅰ)求抛物线E的极坐标方程;
(Ⅱ)过点![]() 倾斜角为
倾斜角为![]() 的直线l交E于M,N两点,若
的直线l交E于M,N两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com