
���� ��1�������⣬$\frac{1}{e}$N0=N0e-5�����Ӷ���æˣ�
��2���ɣ�1��֪��N��t��=N0${e}^{-\frac{1}{5}t}$��N0${e}^{-\frac{1}{5}t}$��N010%�����t��12���Ӷ��õ���Сֵ��
��� �⣺��1�������⣬N��0��=N0��N��5��=$\frac{1}{e}$N0��
��$\frac{1}{e}$N0=N0e-5����
����=$\frac{1}{5}$��
��2���ɣ�1��֪��N��t��=N0${e}^{-\frac{1}{5}t}$��
N0${e}^{-\frac{1}{5}t}$��N010%��
��ã�t��12��
����Ⱦ����ٵ�10%������Ҫ12Сʱ��
���� ���⿼���˺�����ʵ�������е�Ӧ�ã�ͬʱ�����˶������㣬�����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �ڢ� | C�� | �٢� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��$\frac{10}{3}$] | B�� | [2��$\frac{10}{3}$] | C�� | ��2��+�ޣ� | D�� | [$\frac{10}{3}$��+��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
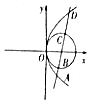 ��ͼ��������C1��y2=2x��ԲC2����x-$\frac{1}{2}$��2+y2=$\frac{1}{4}$������p��0��ֱ��l����C1�Ľ��㣬���ν�C1��C2��A��B��C��D�ĵ㣬��$\overrightarrow{AB}$•$\overrightarrow{CD}$��ֵΪ$\frac{1}{4}$��
��ͼ��������C1��y2=2x��ԲC2����x-$\frac{1}{2}$��2+y2=$\frac{1}{4}$������p��0��ֱ��l����C1�Ľ��㣬���ν�C1��C2��A��B��C��D�ĵ㣬��$\overrightarrow{AB}$•$\overrightarrow{CD}$��ֵΪ$\frac{1}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2-x | B�� | y=x-$\frac{1}{x}$ | C�� | y=-$\frac{1}{{x}^{2}}$ | D�� | y=-tanx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
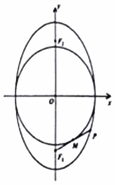 ��F1��F2����ԲC��$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1��0��m��9�����������㣬Բ�ϴ���һ��P����������Բ����Ϊֱ����Բ���߶�PF1�����ڸ��߶ε��е㣮
��F1��F2����ԲC��$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1��0��m��9�����������㣬Բ�ϴ���һ��P����������Բ����Ϊֱ����Բ���߶�PF1�����ڸ��߶ε��е㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com