
分析 (Ⅰ)利用余弦定理列出关系式,把cosA与a的值代入并利用基本不等式求出bc的最大值,即可确定出△ABC面积S的最大值;
(Ⅱ)原式利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可确定出范围.
解答 解:(Ⅰ)∵在△ABC中,A=$\frac{π}{3}$,a=2,
∴由余弦定理a2=b2+c2-2bccosA,得4=b2+c2-bc≥2bc-bc=bc,即bc≤4,
∴S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc≤$\sqrt{3}$,
则S的最大值为$\sqrt{3}$;
(Ⅱ)sinB+cosB=$\sqrt{2}$sin(B+$\frac{π}{4}$),
∵A=$\frac{π}{3}$,A+B+C=π,
∴0<B<$\frac{2π}{3}$,即$\frac{π}{4}$<B+$\frac{π}{4}$<$\frac{11π}{12}$,
∴sin$\frac{11π}{12}$<sin(B+$\frac{π}{4}$)≤sin$\frac{π}{2}$,
∴$\frac{\sqrt{6}-\sqrt{2}}{4}$<sin(B+$\frac{π}{4}$)≤1,
则$\frac{\sqrt{3}-1}{4}$<sinB+cosB≤$\sqrt{2}$.
点评 此题考查了余弦定理,三角形面积公式,以及正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个白球;都是白球 | B. | 两个白球;至少有一个红球 | ||
| C. | 红球、白球各一个;都是白球 | D. | 红球、白球各一个;至少有一个白球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
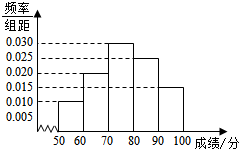 对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )| A. | 0.09 | B. | 0.20 | C. | 0.25 | D. | 0.40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com