
【题目】已知函数![]() (其中
(其中![]() 为常数且
为常数且![]() )在
)在![]() 处取得极值.
处取得极值.
(1)当![]() 时,求
时,求![]() 的极大值点和极小值点;
的极大值点和极小值点;
(2)若![]() 在
在![]() 上的最大值为1,求
上的最大值为1,求![]() 的值.
的值.
【答案】(Ⅰ)单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() ; (Ⅱ)
; (Ⅱ)![]() 或
或![]() .
.
【解析】
试题分析:(1)通过求解函数的导数,结合函数的极值点,求出![]() ,然后通过函数的单调性求解极值点即可;(2)令
,然后通过函数的单调性求解极值点即可;(2)令![]() ,求出
,求出![]() ,
,![]() ,然后讨论当
,然后讨论当![]() 时,得出
时,得出![]() 的单调区间,求出
的单调区间,求出![]() 的最大值,求出
的最大值,求出![]() ;再讨论
;再讨论![]() 时,当
时,当![]() ,
,![]() 及
及![]() 时,分别得出
时,分别得出![]() 的单调区间,求出
的单调区间,求出![]() 的最大值,即可求出
的最大值,即可求出![]() 的值.
的值.
试题解析:(1)∵![]()
∴![]() .
.
∵函数![]() 在
在![]() 处取得极值,
处取得极值,
∴![]()
∴当![]() 时,
时,![]() ,则
,则![]()
![]() 、
、![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
|
| 极大值 |
| 极小值 |
|
∴![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]()
∴![]() 的极大值点为
的极大值点为![]() ,
,![]() 的极小值点为1.
的极小值点为1.
(2)∵![]()
令![]() 得,
得,![]() ,
,![]()
∵![]() 在
在![]() 处取得极值
处取得极值
∴![]()
(ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,则
,则![]() ,即
,即![]()
∴![]()
(ⅱ)当![]() 时,
时,![]()
①当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
∴![]() 的最大值1可能在
的最大值1可能在![]() 或
或![]() 处取得,
处取得,
而![]()
∴![]()
∴![]()
②当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
∴![]() 的最大值1可能在
的最大值1可能在![]() 或
或![]() 处取得,而
处取得,而![]()
∴![]() ,即
,即![]() ,与
,与![]()
③当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 的最大值1可能在
的最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾.
,矛盾.
综上所述,![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:
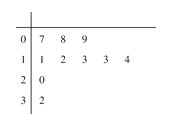
(Ⅰ)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数X的分布列与数学期望;
(Ⅱ)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为一阶的可能性最大,求
户月用水量为一阶的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量![]() 对应的复数为1+2i,向量
对应的复数为1+2i,向量![]() 对应的复数为3-i.
对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业加工生产一批珠宝,要求每件珠宝都按统一规格加工,每件珠宝的原材料成本为3.5万元,每件珠宝售价(万元)与加工时间![]() (单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间
(单位:天)之间的关系满足图1,珠宝的预计销量(件)与加工时间![]() (天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
(天)之间的关系满足图2.原则上,单件珠宝的加工时间不能超过55天,企业支付的工人报酬为这批珠宝销售毛利润的三分之一,其他成本忽略不计算.
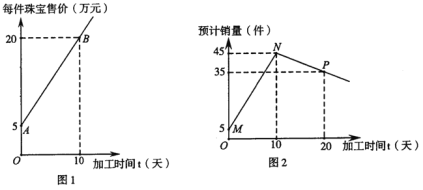
(1)如果每件珠宝加工天数分别为6,12,预计销量分别会有多少件?
(2)设工厂生产这批珠宝产生的纯利润为![]() (万元),请写出纯利润
(万元),请写出纯利润![]() (万元)关于加工时间
(万元)关于加工时间![]() (天)之间的函数关系式,并求纯利润
(天)之间的函数关系式,并求纯利润![]() (万元)最大时的预计销量.
(万元)最大时的预计销量.
注:毛利润=总销售额-原材料成本,纯利润=毛利润-工人报酬
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数
为参数![]() 以原点为极点x轴正半轴为极轴建立极坐标系,直线
以原点为极点x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数,![]() .
.
(1)画出![]() 的大致图象,并根据图象写出函数
的大致图象,并根据图象写出函数![]() 的单调区间;
的单调区间;
(2)当![]() 且
且![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)是否存在实数a,b,![]() 使得函数
使得函数![]() 在
在![]() 上的值域也是
上的值域也是![]() ?若存在,求出a,b的值,若不存在,说明理由.
?若存在,求出a,b的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com