
在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
区域 A B C D
人数 20 10 5 15
(1)求这2人来自同一区域的概率;
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
(1)  ;(2)分布列详见解析,数学期望
;(2)分布列详见解析,数学期望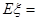
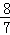
【解析】
试题分析:(1)从50名队员中随机抽出2人去完成一项特殊任务,且2人来自同一区域分为四种情况,分别求概率,再根据互斥事件的概率求和公式计算;(2)基本事件总数为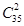 ,
,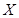 的取值有三种情况:当
的取值有三种情况:当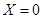 时,那么所选的两人都来自于D,有
时,那么所选的两人都来自于D,有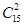 种;当
种;当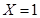 时,一人来自于A,一人来自于D,有
时,一人来自于A,一人来自于D,有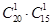 种;当
种;当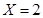 时,所选两人全部来自于A,有
时,所选两人全部来自于A,有 ,分别计算其概率,并写出随机变量
,分别计算其概率,并写出随机变量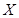 分布列,进而再求数学期望.
分布列,进而再求数学期望.
试题解析:(1)记“这2人来自同一区域”为事件E,那么P(E)=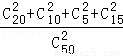 =
= ,
,
所以这2人来自同一区域的概率是 .
.
(2)随机变量ξ可能取的值为0,1,2,且
P(X=0)=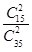 =
=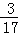 ,P(X =1)=
,P(X =1)=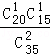 =
=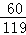 ,P(X =2)=
,P(X =2)=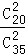 =
=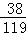
所以ξ的分布列是:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
ξ的数学期望为Eξ=0×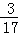 +1×
+1×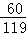 +2×
+2×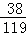 =
=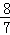
考点:1、古典概型和互斥事件的概率;2、离散型随机变量的分布列和期望.


科目:高中数学 来源: 题型:
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南师大附中高考适应性月考数学试卷5(理科)(解析版) 题型:解答题
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com