
【题目】已知函数![]() 有两个零点
有两个零点![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)记![]() 的极值点为
的极值点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求导得![]() ,分类讨论求出函数的单调性,从而可求出答案;
,分类讨论求出函数的单调性,从而可求出答案;
(2)由题意得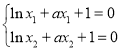 ,则
,则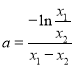 ,令函数
,令函数![]() ,则
,则![]() ,利用导数可求得
,利用导数可求得![]() ,从而可得
,从而可得![]() ,可得
,可得![]() ,要证
,要证![]() ,只需
,只需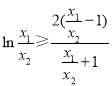 ,令
,令![]() ,即证
,即证![]() ,令
,令![]() ,求导后得函数的单调性与最值,由此可证结论.
,求导后得函数的单调性与最值,由此可证结论.
解:(1)因为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,至多只有一个零点,不符合题意,舍去;
单调递增,至多只有一个零点,不符合题意,舍去;
当![]() 时,若
时,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,
,
因为![]() 有两个零点,所以必须
有两个零点,所以必须![]() ,则
,则![]() ,
,
所以![]() ,解得
,解得![]() ,
,
又因为![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 和
和![]() 各有一个零点,符合题意,
各有一个零点,符合题意,
综上,![]() ;
;
(2)由(1)知![]() ,且
,且![]() ,
,
因为![]() 的两个零点为
的两个零点为![]() ,所以
,所以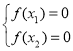 ,所以
,所以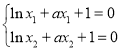 ,
,
解得![]() ,令
,令![]() 所以
所以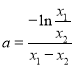 ,
,
令函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
要证![]() ,只需
,只需![]() ,
,
即证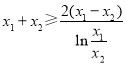 ,即证
,即证![]() ,即证
,即证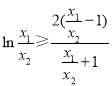 ,
,
令![]() ,再令
,再令![]() ,即证
,即证![]() ,
,
令![]() ,则
,则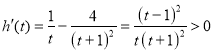 ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,
所以![]() ,原题得证.
,原题得证.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
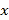
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式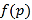 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() (
(![]() 为坐标原点).
为坐标原点).

(1)证明:动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴)与直线
轴)与直线![]() 相交于点
相交于点![]() ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
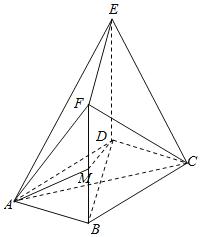
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,点
,点![]() ,过
,过![]() 的直线
的直线![]() 与圆
与圆![]() 交于点
交于点![]() ,过
,过![]() 做直线
做直线![]() 平行
平行![]() 交
交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() y2=1(m>1)的离心率为
y2=1(m>1)的离心率为![]() ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,四边形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分别是线段 SC,AB 上的一点,
.E,F 分别是线段 SC,AB 上的一点, ![]() .
.

(1)求证:![]() 平面SAD;
平面SAD;
(2)求平面DEF与平面SBC所成锐二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面PCD,底面ABCD为梯形,
平面PCD,底面ABCD为梯形,![]() ,
,![]() ,M为PD的中点,过A,B,M的平面与PC交于N.
,M为PD的中点,过A,B,M的平面与PC交于N.![]() ,
,![]() ,
,![]() ,
,![]() .
.
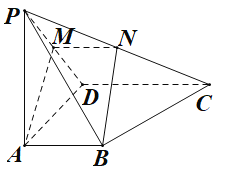
(1)求证:N为PC中点;
(2)求证:![]() 平面PCD;
平面PCD;
(3)T为PB中点,求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com