
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:①对任意
满足:①对任意![]() ,存在正常数
,存在正常数![]() ,都有
,都有![]() 成立;②
成立;②![]() 的值域为
的值域为![]() (
(![]() ),则函数
),则函数![]() 是( )
是( )
A.周期为2的周期函数B.周期为4的周期函数
C.奇函数D.偶函数
科目:高中数学 来源: 题型:
【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的![]() 名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于
名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
|
|
|
|
|
|
| |
男生(人) |
|
|
|
|
|
|
|
女生(人) |
|
|
|
|
|
|
|
(1)完成如下![]() 列联表并判断是否有
列联表并判断是否有![]() 的把握认为了解垃圾分类与性别有关?
的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | ________ | ________ | ________ |
女生 | ________ | ________ | ________ |
合计 | ________ | ________ | ________ |
p>
(2)抽取的![]() 名高中生中按照男、女生采用分层抽样的方法抽取
名高中生中按照男、女生采用分层抽样的方法抽取![]() 人的样本.
人的样本.
(i)求抽取的女生和男生的人数;
(ii)从![]() 人的样本中随机抽取两人,求两人都是女生的概率.
人的样本中随机抽取两人,求两人都是女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
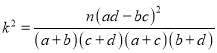 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
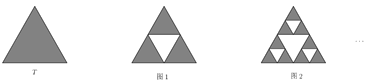
【题目】对于正三角形![]() ,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设
,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设![]() 是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设
是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设![]() 是第
是第![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第1次挖去的中间小三角形面积,
是第1次挖去的中间小三角形面积,![]() 是第2次挖去的三个小三角形面积之和),
是第2次挖去的三个小三角形面积之和),![]() 是前
是前![]() 次挖去的所有三角形的面积之和,则
次挖去的所有三角形的面积之和,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①已知点![]() ,动点
,动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹是一个圆;
的轨迹是一个圆;
②已知![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1;
④在平面直角坐标系内,到点![]() 和直线
和直线![]() 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;
正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]() 到焦点
到焦点![]() 的距离等于3.
的距离等于3.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,设直线
,设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点.
的中点.

(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值;
的值;
(2)设直线![]() 交直线
交直线![]() 于点
于点![]() ,证明:直线
,证明:直线![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是以
是以![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,求整数
,求整数![]() 的值;
的值;
(2)若![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 中是否存在一项
中是否存在一项![]() ,使得
,使得![]() 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续![]() 项的和?请说明理由;
项的和?请说明理由;
(3)若![]() ,
,![]() ,
,![]() (其中
(其中![]() ,且
,且![]() 是
是![]() 的约数),求证:数列
的约数),求证:数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项.
中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十七世纪,法国数学家费马提出猜想;“当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 没有正整数解”,经历三百多年,1995年英国数学家安德鲁
没有正整数解”,经历三百多年,1995年英国数学家安德鲁![]() 怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
①对任意正整数![]() ,关于
,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 都没有正整数解;
都没有正整数解;
②当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
③当正整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
④若关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解,则正整数
至少存在一组正整数解,则正整数![]() ;
;
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com