
【题目】如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
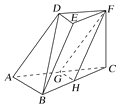
(1)求证:BD∥平面FGH;
(2)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45° ,求平面FGH与平面ACFD所成的角(锐角)的大小.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
试题解析:(Ⅰ)根据![]() 便可得到
便可得到![]() ,从而可以得出四边形
,从而可以得出四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,便有
,便有![]() 平面
平面![]() 再证明
再证明![]() 平面
平面![]() ,从而得到平面B
,从而得到平面B![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]() ;
;
(Ⅱ)连接![]() ,根据条件能够说明
,根据条件能够说明![]() 三直线两两垂直,从而分别以这三直线为
三直线两两垂直,从而分别以这三直线为![]() 轴,建立空间直角坐标系,然后求出一些点的坐标.连接
轴,建立空间直角坐标系,然后求出一些点的坐标.连接![]() ,可说明
,可说明![]() 为平面ACFD的一条法向量,设平面
为平面ACFD的一条法向量,设平面![]() 的法向量为
的法向量为![]()
根据![]() 即可求出法向量
即可求出法向量![]() ,设平面
,设平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,根据
,根据![]() 即可求出平面
即可求出平面![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
证明:
在三棱台DEF-ABC中,
由BC=2EF,H为BC的中点,
可得BH∥EF,BH=EF,
所以四边形BHFE为平行四边形,
可得BE∥HF.在△ABC中,G为AC的中点,H为BC的中点,所以GH∥AB.
又GH∩HF=H,
所以平面FGH∥平面ABED.
因为BD平面ABED,
所以BD∥平面FGH.
(2)解 设AB=2,则CF=1.

在三棱台DEF-ABC中,G为AC的中点,由DF=![]() AC=GC,可得四边形DGCF为平行四边形,
AC=GC,可得四边形DGCF为平行四边形,
因此DG∥FC,又FC⊥平面ABC,所以DG⊥平面ABC.
在△ABC中,由AB⊥BC,∠BAC=45°,G是AC中点.所以AB=BC,GB⊥GC,
因此GB,GC,GD两两垂直.以G为坐标原点,
建立如图所示的空间直角坐标系G-xyz.
所以G(0,0,0),B(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),D(0,0,1).
,0),D(0,0,1).
可得H![]() ,F(0,
,F(0,![]() ,1),
,1),
故![]() =
=![]() ,
,![]() =(0,
=(0,![]() ,1).
,1).
设n=(x,y,z)是平面FGH的一个法向量,
则由 可得
可得![]()
可得平面FGH的一个法向量n=(1,-1,![]() ).
).
因为![]() 是平面ACFD的一个法向量,
是平面ACFD的一个法向量,![]() =(
=(![]() ,0,0).
,0,0).
所以cos〈![]() ,n〉=
,n〉=![]() =
=![]() =
=![]() .
.
所以平面FGH与平面ACFD所成角(锐角)的大小为60°.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知抛物线![]() 的顶点在坐标原点
的顶点在坐标原点![]() ,对称轴为
,对称轴为![]() 轴,焦点为
轴,焦点为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
(Ⅰ)求此抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 做直线
做直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型拟合的效果越好;
越小,说明模型拟合的效果越好;
③散点图中所有点都在回归直线附近;
④随机误差![]() 满足
满足![]() ,其方差
,其方差![]() 的大小可用来衡量预报精确度.
的大小可用来衡量预报精确度.
其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() ,(t为参数).
,(t为参数).
(1)若a=-1,求C与l的交点坐标;
(2)若C上的点到l距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com