练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．函数f（x）=cosx与函数g（x）=loga（$\frac{1}{a}$）x（a＞0且a≠1），则函数F（x）=$\frac{f（x）}{g（x）}$的图象可能是（　　）
    A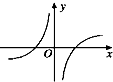．B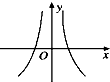．C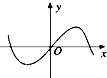．D．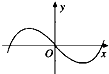

    分析 $g（x）={log_a}{（\frac{1}{a}）^x}={log_a}{a^{-x}}=-x$，$F（x）=\frac{f（x）}{g（x）}=-\frac{cosx}{x}$，定义域为{x|x≠0}，$F（-x）=-\frac{cos（-x）}{-x}=\frac{cosx}{x}=-F（x）$，故函数为奇函数，图象关于原点对称．

    解答 解：$g（x）={log_a}{（\frac{1}{a}）^x}={log_a}{a^{-x}}=-x$$F（x）=\frac{f（x）}{g（x）}=-\frac{cosx}{x}$，
    定义域为{x|x≠0}，排除C，D，
    $F（-x）=-\frac{cos（-x）}{-x}=\frac{cosx}{x}=-F（x）$，故为奇函数，图象关于原点对称，
    故选：A．

    点评 对数式的运算，函数的定义域，奇偶性和函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．函数y=2${\;}^{{x}^{2}-1}$的最小值是$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．圆心在直线2x-3y-1=0上的圆与x轴交于A（1，0），B（3，0）两点，则圆的方程为（　　）
    A．（x-2）2+（y+1）2=2B．（x+2）2+（y-1）2=2C．（x-1）2+（y-2）2=2D．（x-2）2+（y-1）2=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知点F1（-$\sqrt{3}，0$）和F2（$\sqrt{3}，0$）是椭圆M：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的两个焦点，且椭圆M经过点（$\sqrt{3}，\frac{1}{2}$）．
    （1）求椭圆M的方程；
    （2）过点P（0，2）的直线l和椭圆M交于A、B两点，且$\overrightarrow{PB}$=$\frac{3}{5}$$\overrightarrow{PA}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知f（x-1）是偶函数，且在（0，+∞）上单调递增，下列说法正确的是（　　）
    A．$f（{{2^{\frac{1}{x}}}}）＞f（{{{（{\frac{1}{8}}）}^2}}）＞f（{{{log}_2}（{\frac{1}{8}}）}）$B．$f（{{{（{\frac{1}{8}}）}^2}}）＞f（{{2^{\frac{1}{x}}}}）＞f（{{{log}_2}（{\frac{1}{8}}）}）$
    C．$f（{{2^{\frac{1}{x}}}}）＞f（{{{log}_2}（{\frac{1}{8}}）}）＞f（{{{（{\frac{1}{8}}）}^2}}）$D．$f（{{{（{\frac{1}{8}}）}^2}}）＞f（{{{log}_2}（{\frac{1}{8}}）}）＞f（{{2^{\frac{1}{x}}}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知直线l1：y=ax+2a与直线l2：ay=（2a-1）x-a，若l1∥l2，则a=1；若l1⊥l2则a=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，一条准线方程为x=$\frac{8}{3}$$\sqrt{3}$．
    （1）求椭圆C的方程；
    （2）设P（8，0），M，N是椭圆C上关于x轴对称的两个不同的点，连结PN交椭圆C于另一点E，求证：直线ME与x轴相交于定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．把函数y=f（x）的图象向右平移$\frac{π}{6}$个单位，得到$y=2sin（3x-\frac{π}{4}）$的图象，则函数y=f（x）的解析式是y=2sin（3x+$\frac{π}{4}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．观察下列式子：1，1+2+1，1+2+3+2+1，1+2+3+4+3+2+1，…由此可推测出一个一般性的结论：对于n∈N*，1+2+…+n+…+2+1=n2．

    查看答案和解析>>

    同步练习册答案