练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列函数中，既是奇函数，又在区间上递增的是（ ）

    A.B.

    C.D.

    【答案】C

    【解析】

    分析各选项中函数的奇偶性和这些函数在区间上的单调性，从而可得出正确选项.

    对于A选项，设，定义域为，关于原点对称，，该函数为偶函数，且当时，，该函数在区间上为增函数；

    对于B选项，函数的定义域为，不关于原点对称，该函数为非奇非偶函数，且该函数在区间上为增函数；

    对于C选项，设，定义域为，关于原点对称，且，该函数为奇函数，

    由于函数在区间上为增函数，函数在区间上为减函数，

    所以，函数在区间上为增函数；

    对于D选项，设，定义域为，关于原点对称，且，该函数为奇函数，

    由双勾函数的单调性可知，函数在区间上为减函数，在区间上为增函数，则该函数在区间上不单调.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）若关于的不等式在上恒成立，求的取值范围；

    （Ⅱ）设函数，在（Ⅰ）的条件下，试判断在上是否存在极值．若存在，判断极值的正负；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】华东师大二附中乐东黄流中学位于我国南海边，有一片美丽的沙滩和一弯天然的海滨浴场.如图，海岸线MAN，，（海岸线MAN上方是大海），现用长为BC的栏网围成一个三角形学生游泳场所，其中.

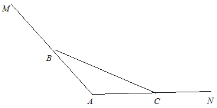
    （1）若，求三角形游泳场所面积最大值；

    （2）若BC=600，，由于学生人数的增加需要扩大游泳场所面积，现在折线MBCN上方选点D，现用长为BD，DC的栏围成一个四边形游泳场所DBAC，使，求四边形游泳场所DBAC的最大面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设F1、F2分别为椭圆C：＝1（a＞b＞0）的左、右焦点，点A为椭圆C的左顶点，点B为椭圆C的上顶点，且|AB|＝，△BF1F2为直角三角形．

    （1）求椭圆C的方程；

    （2）设直线y＝kx+2与椭圆交于P、Q两点，且OP⊥OQ，求实数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为配合“2019双十二”促销活动，某公司的四个商品派送点如图环形分布，并且公司给四个派送点准备某种商品各50个.根据平台数据中心统计发现，需要将发送给四个派送点的商品数调整为40，45，54，61，但调整只能在相邻派送点进行，每次调动可以调整1件商品.为完成调整，则（ ）

    A.最少需要16次调动，有2种可行方案

    B.最少需要15次调动，有1种可行方案

    C.最少需要16次调动，有1种可行方案

    D.最少需要15次调动，有2种可行方案

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，平面，，，的中点为.

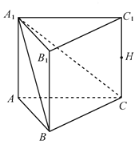
    （Ⅰ）求证：；

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）在棱上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市对城市路网进行改造，拟在原有a个标段(注：一个标段是指一定长度的机动车道)的基础上，新建x个标段和n个道路交叉口，其中n与x满足n＝ax＋5.已知新建一个标段的造价为m万元，新建一个道路交叉口的造价是新建一个标段的造价的k倍．

    (1)写出新建道路交叉口的总造价y(万元)与x的函数关系式；

    (2)设P是新建标段的总造价与新建道路交叉口的总造价之比．若新建的标段数是原有标段数的20%，且k≥3.问：P能否大于，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况，该州教育局组织高三理科生进行了摸底考试，现从参加考试的学生中随机抽取了100名理科生，，将他们的化学成绩（满分为100分）分为6组，得到如图所示的频率分布直方图.

    （1）求a的值；

    （2）记A表示事件“从参加考试的所有理科生中随机抽取一名学生，该学生的化学成绩不低于70分”，试估计事件A发生的概率；

    （3）在抽取的100名理科生中，采用分层抽样的方法从成绩在内的学生中抽取10名，再从这10名学生中随机抽取4名，记这4名理科生成绩在内的人数为X，求X的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若存在正常数，使得对任意的，都有成立，我们称函数为“同比不减函数”．

    （1）求证：对任意正常数，都不是“同比不减函数”；

    （2）若函数是“同比不减函数”，求的取值范围；

    （3）是否存在正常数，使得函数为“同比不减函数”，若存在，求的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案