
 过⊙O外一点P作⊙O的两条割线PAB,PMN,其中PMN过圆心O,过P作再作⊙O的切线PT,切点为T.已知PM=MO=ON=1.
过⊙O外一点P作⊙O的两条割线PAB,PMN,其中PMN过圆心O,过P作再作⊙O的切线PT,切点为T.已知PM=MO=ON=1.分析 (Ⅰ)利用切割线定理求切线PT的长;
(Ⅱ)证明△PAN∽△PBM,△PAM∽△PBN,即可求$\frac{AM•BM}{AN•BN}$时值.
解答 解:(Ⅰ)∵PM=MO=ON=1,
∴PT2=PM•PN=3,
∴PT=$\sqrt{3}$;
(Ⅱ)∵∠ABM=∠ANM,∠BPM=∠NPA,
∴△PAN∽△PBM,
∴$\frac{BM}{AN}=\frac{PB}{PN}$①,
∵∠PAM=∠PNB,∠PMA=∠PBN,
∴△PAM∽△PBN,
∴$\frac{AM}{BN}$=$\frac{PA}{PN}$②
由①②,可知$\frac{AM•BM}{AN•BN}$=$\frac{PA•BP}{P{N}^{2}}$=$\frac{PM•PN}{P{N}^{2}}$=$\frac{1}{3}$.
点评 本题考查切割线定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
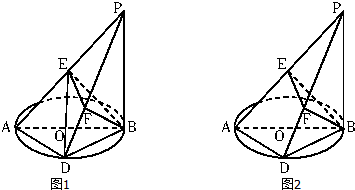
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
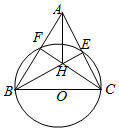 如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:
如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com