
| x |
| 1 |
| y |
| 2 |
| z |
| 1 |
| 7 |
| 3 |
| 7 |
| 3 |
| 7 |
| 3 |


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| 3 |
| 2 |
| a |
| b |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
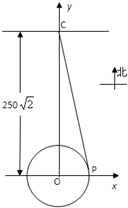 某城市交通规划中,拟在以点O为圆心,半径为50m的高架圆形车道外侧P处开一个出口,以与圆形道相切的方式,引申一条直道连接到距圆形道圆心O正北250
某城市交通规划中,拟在以点O为圆心,半径为50m的高架圆形车道外侧P处开一个出口,以与圆形道相切的方式,引申一条直道连接到距圆形道圆心O正北250| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
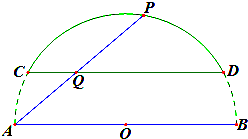 某房地产开发商在其开发的一个小区前面建了一个弓形景观湖,如图,该弓形所在的圆是以AB为直径的圆,已知AB=300m,CD与AB平行且它们之间的距离为50
某房地产开发商在其开发的一个小区前面建了一个弓形景观湖,如图,该弓形所在的圆是以AB为直径的圆,已知AB=300m,CD与AB平行且它们之间的距离为50| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) |
| g(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com