
A.20 B.22 C.24 D.28
科目:高中数学 来源: 题型:
(09年临沭县模块考试理)(12分)
已知数列{an}的前n项和![]() 。
。
(Ⅰ)用n、k表示an;
(Ⅱ)若数列{bn}对任意正整数n,均有(bn+1-bn+2)lna1+(bn+2-bn)lna3+(bn-bn+1)lna5=0,
求证:数列{bn}为等差数列
(Ⅲ)在(Ⅰ)、(Ⅱ)中,设k=1,bn=n+1,xn=a1b1+a2b2+???+anbn,试求数列{xn}的通
项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年济宁质检一理)(14分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,且在点
的图象上,且在点![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中最小的数,
中最小的数,![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年山东实验中学诊断三理)(12分)在数列![]() 中,已知
中,已知
![]()
![]() (1)记
(1)记![]() 求证:数列
求证:数列![]() 是等差数列;
是等差数列;
![]() (2)求数列
(2)求数列![]() 的通项公式;
的通项公式;
![]() (3)对于任意给定的正整数
(3)对于任意给定的正整数![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市徐汇区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(理)对于数列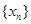 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数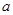 ,公比为正整数
,公比为正整数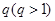 的无穷等比数列
的无穷等比数列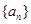 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项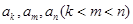 .
.
(1) 若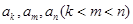 成等比数列,求
成等比数列,求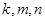 之间满足的等量关系;
之间满足的等量关系;
(2) 他猜想:“在上述数列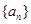 中存在一个子数列
中存在一个子数列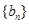 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了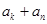 与
与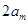 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
(3) 他又想:在首项为正整数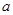 ,公差为正整数
,公差为正整数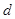 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com