
【题目】如图在直三棱柱ABC A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

(1)求证:DE∥平面AA1C1C;
(2) 求证:BC1⊥AB1;
(3)设AC=BC=CC1 =1,求锐二面角A- B1C- A1的余弦值。
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由DE是△B1AC中位,线易知DE∥AC,从而DE∥平面AA1C1C;(2)先证AC⊥平面BCC1B1,得BC1⊥AC,又因为BC1⊥B1C,所以BC1⊥平面B1AC,所以BC1⊥AB1;(3)先求出点A1到平面B1AC的距离![]() ,再求出点A1到交线B1C的距离
,再求出点A1到交线B1C的距离![]() ,
,![]() ,转化为余弦值即可.
,转化为余弦值即可.
证明:(1)由题意知,E为B1C的中点,
又D为AB1的中点,因此DE∥AC.
又因为DE平面AA1C1C,AC平面AA1C1C,
所以DE∥平面AA1C1C.
(2)因为三棱柱ABC A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1平面BCC1B1,
BC平面BCC1B1,BC∩CC1=C,
所以AC⊥平面BCC1B1.
又因为BC1平面BCC1B1,所以BC1⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.
因为AC,B1C平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.
又因为AB1平面B1AC,所以BC1⊥AB1.
(3)因为A1C1∥AC,AC平面B1AC,A1C1平面B1AC
所以A1C1∥平面B1AC
所以点A1到平面B1AC与点C1到平面B1AC的距离相等,且![]()
又因为在△A1B1C中,A1B1=A1C=B1C=![]() ,
,
所以点A1到直线B1C的距离![]()
所以锐二面角A- B1C- A1的正弦值![]()
所以锐二面角A- B1C- A1的正弦值![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,直线
,直线![]() 是
是![]() 图象的一条对称轴.
图象的一条对称轴.
(1)求![]() 的单调递减区间;
的单调递减区间;
(2)已知函数![]() 的图象是由
的图象是由![]() 图象上的各点的横坐标伸长到原来的4倍,然后再向左平移
图象上的各点的横坐标伸长到原来的4倍,然后再向左平移![]() 个单位长度得到,若
个单位长度得到,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
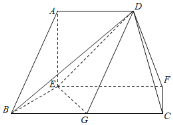
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求二面角C-DF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比数列.可得
成等比数列.可得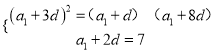 ,解之得即可得出数列
,解之得即可得出数列![]() 的通项公式;
的通项公式;
2)由(1)得![]() ,则
,则![]() ,由裂项相消法可求数列
,由裂项相消法可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,且
,且![]() 由题意得
由题意得![]() ,
,
即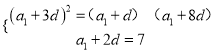 ,解得
,解得![]() ,
,
所以数列![]() 的通项公式
的通项公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【题型】解答题
【结束】
18
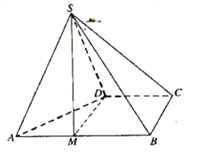
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取![]() 张进行统计,将结果分成5组,分别是
张进行统计,将结果分成5组,分别是![]() ,制成如图所示的频率分布直方图(假设消费金额均在
,制成如图所示的频率分布直方图(假设消费金额均在![]() 元的区间内).
元的区间内).

(1)若在消费金额为![]() 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自![]() 元区间的概率;
元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案:
方案一:全场商品打8.5折;
方案二:全场购物满200元减20元,满400元减50元,满600元减80元,满800元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com