解:(1)

•

=2sin(

-A)sin(

+A)-1
=2sin(

-A)cos(

-A)-1
=sin(

-2A)-1=cos2A-1=-

,
∴cos2A=-

,
∵0<A<

,∴0<2A<π,∴2A=

,A=

设△ABC的外接圆半径为R,由a=2RsinA得2

=2R×

,∴R=2
由b=2RsinB得sinB=

,又b<a,∴B=

,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=

•

+

•

=
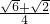
,
∴△ABC的面积为S=

absinC=

•2

•2

•
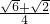
=3+

.
(2)解法1:由a
2=b
2+c
2-2bccosA,得b
2+c
2-bc=12,
∴(b+c)
2=3bc+12≤3(
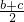
)
2+12,
∴(b+c)
2≤48,即b+c≤4

,(当且仅当b=c时取等号)
从而b+c的最大值为4

.
解法2:由正弦定理得:

=

=

=
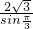
=4,又B+C=π-A=

,
∴b+c=4(sinB+sinC)=4[sinB+sin(

-B)]=6sinB+2

cosB=4

sin(B+

),
∴当B+

=

,即B=

时,b+c取得最大值4

.
分析:(1)通过向量的数量积二倍角的余弦函数,求出A的二倍角的余弦值,然后求出A.通过正弦定理求出R,然后求出三角形的面积.
(2)解法1:由余弦定理a
2=b
2+c
2-2bccosA,结合不等式求出b+c的最大值为4

.
解法2:由正弦定理得:

=

,利用两角和与差的三角函数,根据角的范围,求出b+c的最大值.
点评:本题考查正弦定理与余弦定理,三角形的面积公式,两角和与差的三角函数的应用,考查计算能力,转化思想的应用.

 =(sin(
=(sin( -A),1),
-A),1), =(2sin(
=(2sin( +1),-1),a=2
+1),-1),a=2 ,且
,且 •
• =-
=- .
. ,求△ABC的面积;
,求△ABC的面积; •
• =2sin(
=2sin( -A)sin(
-A)sin( +A)-1
+A)-1 -A)cos(
-A)cos( -A)-1
-A)-1 -2A)-1=cos2A-1=-
-2A)-1=cos2A-1=- ,
, ,
, ,∴0<2A<π,∴2A=
,∴0<2A<π,∴2A= ,A=
,A=
 =2R×
=2R× ,∴R=2
,∴R=2 ,又b<a,∴B=
,又b<a,∴B= ,
, •
• +
+ •
• =
=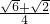 ,
, absinC=
absinC= •2
•2 •2
•2 •
•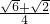 =3+
=3+ .
.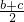 )2+12,
)2+12, ,(当且仅当b=c时取等号)
,(当且仅当b=c时取等号) .
. =
= =
= =
=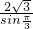 =4,又B+C=π-A=
=4,又B+C=π-A= ,
, -B)]=6sinB+2
-B)]=6sinB+2 cosB=4
cosB=4 sin(B+
sin(B+ ),
), =
= ,即B=
,即B= 时,b+c取得最大值4
时,b+c取得最大值4 .
. .
. =
= ,利用两角和与差的三角函数,根据角的范围,求出b+c的最大值.
,利用两角和与差的三角函数,根据角的范围,求出b+c的最大值.

 阅读快车系列答案
阅读快车系列答案