Question

已知函数f（x）=e^x-x-a．
（1）求函数f（x）的单调区间；
（2）若f（x）≥0对任意x∈R都成立，求g（a）=1+a|a-3|的最大值；
（3）当a＞1时，求关于x的方程e^x-x-a=0的根的个数．

Answer 1

解：（1）f（x）=e^x-x-a，故f′（x）=e^x-1，由f′（x）=e^x-1=0，
得x=0，当x＜0时，f′（x）＜0；当x＞0时，f′（x）＞0，
故函数f（x）的单调减区间为（-∞，0），增区间为（0，+∞）； …（5分）
（2）若f（x）≥0对任意x∈R都成立，则a≤（e^x-x）_min，
由（1）得当求x=0时，（e^x-x）_min=1，故a≤1，
∴，
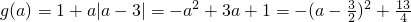
∴当a=1时，g（a）_max=1+|1-3|=3； …（10分）
（3）由（1）得f（x）_min=f（0）=1-a，当a＞1时，f（0）＜0，
又∵f（-a）=e^-a＞0，且x→+∞时，f（x）→+∞，
故关于x的方程e^x-x-a=0的根的个数为2个． …（14分）
分析：（1）直接利用函数的导数，求解函数f（x）的单调区间；
（2）f（x）≥0对任意x∈R都成立，利用（1）推出g（a）=1+a|a-3|的表达式，然后通过二次函数求出表达式的最大值；
（3）利用（1）当a＞1时，结合函数的最值，函数的单调性推出关于x的方程e^x-x-a=0的根的个数．
点评：本题考查函数的导数判断函数的单调性，函数的最值的应用，考查函数的零点，考查分析问题解决问题的能力．
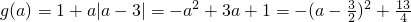