
如图,底面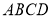 是边长为2的菱形,且
是边长为2的菱形,且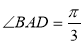 ,以
,以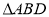 与
与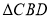 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥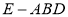 与
与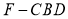 ,且
,且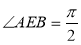 .
.
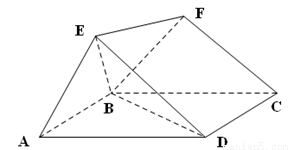
(1)求证: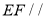 平面
平面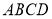 ;
;
(2)求多面体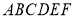 的体积.
的体积.
科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
如图是函数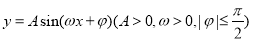 图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点
图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点
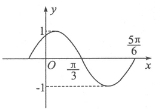
A.向左平移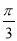 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的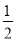 ,纵坐标不变
,纵坐标不变
B.向左平移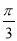 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移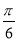 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的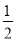 ,纵坐标不变
,纵坐标不变
D.向左平移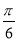 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷(解析版) 题型:选择题
设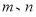 是不同的直线,
是不同的直线,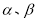 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①若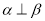 ,
,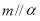 ,则
,则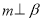
②若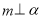 ,
,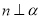 ,则
,则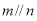
③若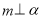 ,
,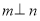 ,则
,则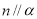
④若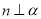 ,
,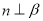 ,则
,则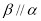 .
.
其中真命题的序号为( )
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:填空题
空间中任意放置的棱长为2的正四面体 .下列命题正确的是_________.(写出所有正确的命题的编号)
.下列命题正确的是_________.(写出所有正确的命题的编号)
①正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
②正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
③正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
⑤正四面体 的主视图面积可能是
的主视图面积可能是
⑥正四面体 的主视图面积可能是
的主视图面积可能是 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:选择题
若 ,且
,且
 则“
则“ ”是“
”是“ ”的( )
”的( )
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省合肥市高三第二次教学质量检测理科数学试卷(解析版) 题型:选择题
已知函数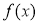 满足:对定义域内的任意
满足:对定义域内的任意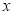 ,都有
,都有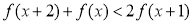 ,则函数
,则函数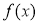 可以是( )
可以是( )
A.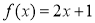 B.
B.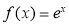 C.
C.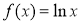 D.
D.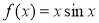
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com