解:(1)设D(x,y),A(a,a),B(b,-b),
∵D是AB的中点,∴x=
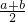
,y=
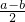
,
∵|AB|=2

,∴(a-b)
2+(a+b)
2=12,
∴(2y)
2+(2x)
2=12,∴点D的轨迹C的方程为x
2+y
2=3.
(2)①当直线l与x轴垂直时,P(1,

),Q(1,-

),
此时|PQ|=2

,不符合题意;
当直线l与x轴不垂直时,设直线l的方程为y=k(x-1),
由于|PQ|=3,所以圆心C到直线l的距离为

,
由

=

,解得k=
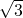
.故直线l的方程为y=
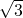
(x-1).
②当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),
由消去y得(k
2+1)x
2-2k
2x+k
2-3=0,
设P(x
1,y
1),Q(x
2,y
2)则由韦达定理得x
1+x
2=

,x
1x
2=

,
则

=(m-x
1,-y
1),

=(m-x
2,-y
2),
∴

•

=(m-x
1)(m-x
2)+y
1y
2=m
2-m(x
1+x
2)+x
1x
2+y
1y
2
=m
2-m(x
1+x
2)+x
1x
2+k
2(x
1-1)(x
2-1)
=m
2-

+

+k
2(

-

+1)=
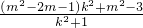
要使上式为定值须
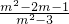
=1,解得m=1,
∴

•

为定值-2,
当直线l的斜率不存在时P(1,

),Q(1,-

),
由E(1,0)可得

=(0,-

),

=(0,

),
∴

•

=-2,
综上所述当E(1,0)时,

•

为定值-2.
分析:(1)设D(x,y),A(a,a),B(b,-b),通过D是AB的中点,|AB|的距离,列出方程即可求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,通过直线的斜率存在与不存在分别求解,利用圆心到直线的距离求出直线的斜率,然后求直线l的方程;
②当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),推出(k
2+1)x
2-2k
2x+k
2-3=0,
由韦达定理以及

•

,确定

•

为定值-2,当直线l的斜率不存在时,求出P(1,

),Q(1,-

),
得到

•

=-2,即可求出

•

恒为定值时E点的坐标及定值.
点评:本题考查直线与圆心位置关系,数量积与韦达定理的应用,轨迹方程的求法,考查计算能力,分类讨论思想.

 ,D是AB的中点.
,D是AB的中点. •
• 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.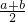 ,y=
,y=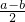 ,
, ,∴(a-b)2+(a+b)2=12,
,∴(a-b)2+(a+b)2=12, ),Q(1,-
),Q(1,- ),
), ,不符合题意;
,不符合题意; ,
, =
= ,解得k=
,解得k=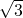 .故直线l的方程为y=
.故直线l的方程为y=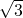 (x-1).
(x-1). ,x1x2=
,x1x2= ,
, =(m-x1,-y1),
=(m-x1,-y1), =(m-x2,-y2),
=(m-x2,-y2), •
• =(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2
=(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2 +
+ +k2(
+k2( -
- +1)=
+1)=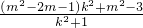
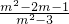 =1,解得m=1,
=1,解得m=1, •
• 为定值-2,
为定值-2, ),Q(1,-
),Q(1,- ),
), =(0,-
=(0,- ),
), =(0,
=(0, ),
), •
• =-2,
=-2, •
• 为定值-2.
为定值-2. •
• ,确定
,确定 •
• 为定值-2,当直线l的斜率不存在时,求出P(1,
为定值-2,当直线l的斜率不存在时,求出P(1, ),Q(1,-
),Q(1,- ),
), •
• =-2,即可求出
=-2,即可求出 •
• 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.

 口算能手系列答案
口算能手系列答案