
【题目】设函数![]() ,
,![]() .
.
(1)![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(3)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
【答案】(1) y=0.
(2)![]() .
.
(3)![]() .
.
【解析】分析:(1)先利用导数求切线的斜率,再写出切线的方程.(2)先求导得![]() ,转化为
,转化为![]() 与
与![]() 的图像的交点有两个,再利用数形结合分析两个函数的图像得到
的图像的交点有两个,再利用数形结合分析两个函数的图像得到![]() 的取值范围.(3)先转化为当
的取值范围.(3)先转化为当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,再构造函数
,再构造函数![]() 求其最小值,令其最小值大于零,得a的取值范围.
求其最小值,令其最小值大于零,得a的取值范围.
详解:(1)由题得![]() 所以切线方程为y=0.
所以切线方程为y=0.
(2) 当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 有两个极值点就是方程
有两个极值点就是方程![]() 有两个解,
有两个解,
即![]() 与
与![]() 的图像的交点有两个.
的图像的交点有两个.
∵![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.![]() 有极大值
有极大值![]() 又因为
又因为![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
当![]() 时
时![]() 与
与![]() 的图像的交点有0个;
的图像的交点有0个;
当![]() 或
或![]() 时
时![]() 与
与![]() 的图像的交点有1个;
的图像的交点有1个;
当![]() 时
时![]() 与
与![]() 的图象的交点有2个;
的图象的交点有2个;
综上![]() .
.
(3)函数![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,
轴平行,
所以![]() 且
且![]() ,因为
,因为![]() ,
,
所以![]() 且
且![]() ;
;
![]() 在
在![]() 时,其图像的每一点处的切线的倾斜角均为锐角,
时,其图像的每一点处的切线的倾斜角均为锐角,
即当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,
,
令![]() ,∴
,∴![]()
设![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 单调递增,即
单调递增,即![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,当
,当![]() 且
且![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增;
单调递增;
∴![]() 成立
成立
当![]() ,因为
,因为![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,![]() ,
,
所以存在![]() 有
有![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减,所以有
单调递减,所以有![]() ,
,![]() 不恒成立;
不恒成立;
所以实数![]() 的取值范围为
的取值范围为![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数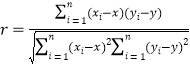 ;
;
回归直线方程为![]() ,其中
,其中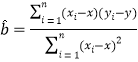 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知点![]() ,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.

(1)若直线OA的方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() :
:![]() 上有一动点
上有一动点![]() ,
,![]() 到椭圆
到椭圆![]() 的两焦点
的两焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,
,![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,
,![]() (
(![]() 为坐标原点)且
为坐标原点)且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)请作出该函数在长度为一个周期的闭区间的大致图象;
(2)试判断该函数的奇偶性,并运用函数的奇偶性定义说明理由;
(3)求该函数的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C方程:![]() +
+![]() =1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
=1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
(1)若椭圆的离心率为e,证明|MF|=a﹣ex0;
(2)已知不过焦点F的直线l与圆x2+y2=b2相切于点Q,并与椭圆C交于A,B两点,且A,B两点都在y轴的右侧,若a=2,求△ABF的周长.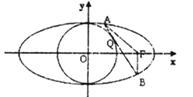
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com