
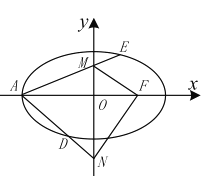
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() 为原点,
为原点, ![]() ,
, ![]() 是
是![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.

(Ⅰ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅱ)证明: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
【答案】(1)1;(2)详见解析。
【解析】试题分析:(Ⅰ)设![]() ,
, ![]() ,然后根据
,然后根据![]() 求得
求得![]() 的值,从而得到
的值,从而得到![]() 的表达式,从而利用基本不等式求出最小值,;(Ⅱ)首先设出直线
的表达式,从而利用基本不等式求出最小值,;(Ⅱ)首先设出直线![]() 的方程,然后联立椭圆方程,利用韦达定理得到点
的方程,然后联立椭圆方程,利用韦达定理得到点![]() 坐标间的关系,从而使问题得证.
坐标间的关系,从而使问题得证.
试题解析:(Ⅰ)设![]() ,
, ![]() ,∵
,∵![]() ,可得
,可得![]() ,
,
![]() ,
,
∵![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积的最小值为1.
的面积的最小值为1.
(Ⅱ)∵![]() ,
, ![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
由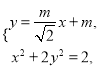 得
得![]() ,
,
由![]() ,得
,得![]() ,①
,①
同理可得![]() ,
,
∵![]() ,∵
,∵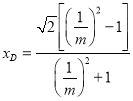
![]() ②
②
故由①②可知: ![]() ,
,
代入椭圆方程可得![]()
∵![]() ,故
,故![]() ,
, ![]() 分别在
分别在![]() 轴两侧,
轴两侧, ![]() ,
,
∴![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
点睛:解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 满足
满足 ![]() (其中
(其中 ![]() ,
, ![]() ).
).
(1)求 ![]() 的表达式;
的表达式;
(2)对于函数 ![]() ,当
,当 ![]() 时,
时, ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
(3)当 ![]() 时,
时, ![]() 的值为负数,求
的值为负数,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2016年1月1日起全国统一实施全面两孩政策. 为了解适龄民众对放开
生二胎政策的态度,某市选取70后作为调查对象,随机调查了10人,其中打算生二胎
的有4人,不打算生二胎的有6人.
(1)从这10人中随机抽取3人,记打算生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若以这10人的样本数据估计该市的总体数据,且以频率作为概率,从该市70后中随机抽取3人,记打算生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ).
).
(1)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的极值点;
的极值点;
(3)令![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上相异三点,其中
上相异三点,其中![]() .求证:
.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系.某重点高中数学教师对高三年级的50名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有22人,余下的人中,在高三年级模拟考试中数学平均成绩不足120分钟的占![]() ,统计成绩后,得到如下
,统计成绩后,得到如下![]() 的列联表:
的列联表:
分数大于等于120分钟 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 22 | |
周做题时间不足15小时 | |||
合计 | 50 |
(Ⅰ)请完成上面的![]() 列联表,并判断能否有99%以上的把握认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否有99%以上的把握认为“高中生的数学成绩与学生自主学习时间有关”;
(Ⅱ)(ⅰ)按照分层抽样,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为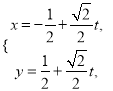 椭圆
椭圆![]() 的参数方程为
的参数方程为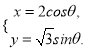 在以坐标原点为极点,
在以坐标原点为极点, ![]() 轴正半轴为极轴建立的极坐标系中,点
轴正半轴为极轴建立的极坐标系中,点![]() 的坐标为
的坐标为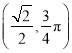 .
.
(1)将点![]() 的坐标化为直角坐标系下的坐标,椭圆的参数方程化为普通方程;
的坐标化为直角坐标系下的坐标,椭圆的参数方程化为普通方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com