
【题目】某股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上,该股票在30天内的日交易量
落在如图所示的两条线段上,该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如表所示:
(天)的部分数据如表所示:
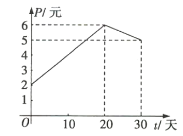
![]()
(1)根据提供的图象,写出该股票每股的交易价格![]() 与时间
与时间![]() 所满足的函数关系式;
所满足的函数关系式;
(2)根据表中数据确定日交易量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(3)在(1)(2)的结论下,若该股票的日交易额为![]() (万元),写出
(万元),写出![]() 关于
关于![]() 的函数关系式,并求在这30天中第几天的交易额最大,最大是多少?
的函数关系式,并求在这30天中第几天的交易额最大,最大是多少?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从1到100这100个自然数中,每次取出不同的两个数,使它们的和大于100,不同取法共有( )种.
A. 50 B. 100 C. 1275 D. 2500
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题![]() “
“![]() ,
,![]() ”,则
”,则![]() 是真命题
是真命题
B. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C. 命题“![]() ,
,![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”
”
D. “![]() ”是“
”是“![]() 在
在![]() 上为增函数”的充要条件
上为增函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本![]() (万元)可以看成月产量
(万元)可以看成月产量![]() (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本![]() (万元)关于月产量
(万元)关于月产量![]() (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.
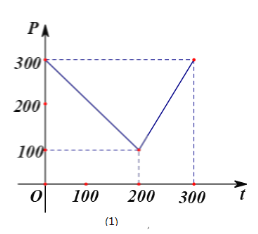
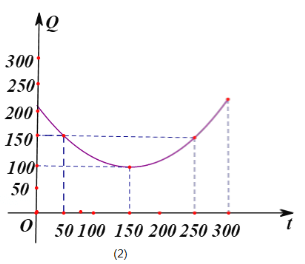
(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(﹣4,4)上的奇函数,满足f(2)=1,当﹣4<x≤0时,有f(x)=![]() .
.
(1)求实数a,b的值;
(2)求函数f(x)在区间(0,4)上的解析式,并利用定义证明其在该区间上的单调性;
(3)解关于m的不等式f(m2+1)+![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解创建文明城市过程中学生对创建工作的满意情况,相关部门对某中学的100名学生进行调查.得到如下的统计表:
满意 | 不满意 | 合计 | |
男生 | 50 |
|
|
女生 |
| 15 |
|
合计 |
|
| 100 |
已知在全部100名学生中随机抽取1人对创建工作满意的概率为![]() .
.
(1)在上表中![]() 相应的数据依次为;
相应的数据依次为;
(2)是否有充足的证据说明学生对创建工作的满意情况与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将所得图象的纵坐标不变,横坐标伸长到原来的2倍,得到的函数
个单位后,再将所得图象的纵坐标不变,横坐标伸长到原来的2倍,得到的函数![]() 的图象关于
的图象关于![]() 轴对称,求
轴对称,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=![]() ,x∈(-2,2).
,x∈(-2,2).
(1) 判断f(x)的奇偶性并说明理由;
(2) 求证:函数f(x)在(-2,2)上是增函数;
(3) 若f(2+a)+f(1-2a)>0,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com