
ЁОЬтФПЁПЯТБэЬсЙЉСЫФГГЇНкФмНЕКФММЪѕИФдьКѓЩњВњМзВњЦЗЙ§ГЬжаМЧТМЕФВњСПЃЈ![]() ЖжЃЉгыЯргІЕФЩњВњФмКФ
ЖжЃЉгыЯргІЕФЩњВњФмКФ![]() ЃЈЖжЃЉБъзМУКЕФМИзщЖдееЪ§ОнЃК
ЃЈЖжЃЉБъзМУКЕФМИзщЖдееЪ§ОнЃК
|
|
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЧыЛГіЩЯБэЪ§ОнЕФЩЂЕуЭМЃЛВЂжИГі![]() ЪЧЗёЯпадЯрЙиЃЛ
ЪЧЗёЯпадЯрЙиЃЛ
ЃЈ2ЃЉЧыИљОнЩЯБэЬсЙЉЕФЪ§ОнЃЌгУзюаЁЖўГЫЗЈЧѓГі![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]()
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉвбжЊИУГЇММЪѕИФдьЧА![]() ЖжМзВњЦЗФмКФЮЊ
ЖжМзВњЦЗФмКФЮЊ![]() ЖжБъзМУКЃЌЪдИљОнЧѓГіЕФЯпадЛиЙщЗНГЬЃЌдЄВтЩњВњ
ЖжБъзМУКЃЌЪдИљОнЧѓГіЕФЯпадЛиЙщЗНГЬЃЌдЄВтЩњВњ![]() ЖжМзВњЦЗЕФЩњВњФмКФБШММЪѕИФдьЧАНЕЕЭЖрЩйЖжБъзМУКЃП
ЖжМзВњЦЗЕФЩњВњФмКФБШММЪѕИФдьЧАНЕЕЭЖрЩйЖжБъзМУКЃП
ЃЈВЮПМ:гУзюаЁЖўГЫЗЈЧѓЯпадЛиЙщЗНГЬЯЕЪ§ЙЋЪН ЃЌ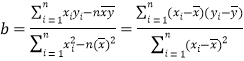 ,
, ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉЩЂЕуЭММћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбЫљИјЕФЫФЖдЪ§ОнаДГЩЖдгІЕФЕуЕФзјБъЃЌдкзјБъЯЕжаУшГіРДЃЌЕУЕНЩЂЕуЭМЃЌгЩЭМПЩжЊГі![]() ЪЧЯпадЯрЙиЃЛЃЈ2ЃЉИљОнЫљИјЕФетзщЪ§ОнЧѓГібљБОжааФЕуЕФзјБъЃЌРћгУЙЋЪНЃЌ
ЪЧЯпадЯрЙиЃЛЃЈ2ЃЉИљОнЫљИјЕФетзщЪ§ОнЧѓГібљБОжааФЕуЕФзјБъЃЌРћгУЙЋЪНЃЌ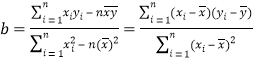 ,ЛиЙщЗНГЬЕФЯЕЪ§ЃЌЕУЕНЯпадЛиЙщЗНГЬЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЃЌМЦЫу
,ЛиЙщЗНГЬЕФЯЕЪ§ЃЌЕУЕНЯпадЛиЙщЗНГЬЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЃЌМЦЫу![]() ЪБЕФЩњВњФмКФЃЌНјЖјПЩЧѓГіБШММИФЧАНЕЕЭЕФБъзМУК.
ЪБЕФЩњВњФмКФЃЌНјЖјПЩЧѓГіБШММИФЧАНЕЕЭЕФБъзМУК.
ЪдЬтНтЮіЃКЃЈ1ЃЉАбЫљИјЕФЫФЖдЪ§ОнаДГЩЖдгІЕФЕуЕФзјБъЃЌдкзјБъЯЕжаУшГіРДЃЌЕУЕНЩЂЕуЭМШчЭМЃК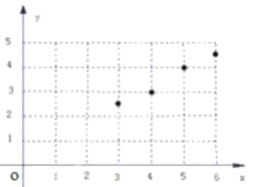 ЃЌгЩЭМПЩжЊГі
ЃЌгЩЭМПЩжЊГі![]() ЪЧЯпадЯрЙи
ЪЧЯпадЯрЙи
ЃЈ2ЃЉгЩЖдееЪ§ОнЃЌМЦЫуЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЛиЙщЗНГЬЯЕЪ§ЮЊ
ЛиЙщЗНГЬЯЕЪ§ЮЊ![]()
![]() ЃЌ
ЃЌ![]()
![]() ,
,![]() ЫљЧѓЯпадЛиЙщЗНГЬЮЊ
ЫљЧѓЯпадЛиЙщЗНГЬЮЊ![]()
![]() .
.
ЃЈ3ЃЉгЩЃЈ2ЃЉЕФЯпадЛиЙщЗНГЬЃЌЙРМЦЩњВњ![]() ЖжМзВњЦЗЕФЩњВњФмКФЮЊ
ЖжМзВњЦЗЕФЩњВњФмКФЮЊ![]() ЃЈЖжЃЉЃЌ
ЃЈЖжЃЉЃЌ![]() ЖжЃЌдЄВтБШММИФЧАНЕЕЭСЫ
ЖжЃЌдЄВтБШММИФЧАНЕЕЭСЫ![]() ЖжБъзМУК.
ЖжБъзМУК.
ЁОЗНЗЈЕуЧчЁПБОЬтжївЊПМВщЩЂЕуЭМЕФЛЗЈКЭЯпадЛиЙщЗНГЬЃЌЪєгкФбЬт.ЧѓЛиЙщжБЯпЗНГЬЕФВНжшЃКЂйвРОнбљБОЪ§ОнЛГіЩЂЕуЭМЃЌШЗЖЈСНИіБфСПОпгаЯпадЯрЙиЙиЯЕЃЛЂкМЦЫу![]() ЕФжЕЃЛЂлМЦЫуЛиЙщЯЕЪ§
ЕФжЕЃЛЂлМЦЫуЛиЙщЯЕЪ§![]() ЃЛЂмаДГіЛиЙщжБЯпЗНГЬЮЊ
ЃЛЂмаДГіЛиЙщжБЯпЗНГЬЮЊ![]() ЃЛ ЛиЙщжБЯпЙ§бљБОЕужааФ
ЃЛ ЛиЙщжБЯпЙ§бљБОЕужааФ![]() ЪЧвЛЬѕживЊаджЪЃЌРћгУЯпадЛиЙщЗНГЬПЩвдЙРМЦзмЬхЃЌАяжњЮвУЧЗжЮіСНИіБфСПЕФБфЛЏЧїЪЦ.
ЪЧвЛЬѕживЊаджЪЃЌРћгУЯпадЛиЙщЗНГЬПЩвдЙРМЦзмЬхЃЌАяжњЮвУЧЗжЮіСНИіБфСПЕФБфЛЏЧїЪЦ.


 ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаДэЮѓЕФЪЧЃЈ ЃЉ
A. ШчЙћЦНУц![]() ВЛДЙжБгкЦНУц
ВЛДЙжБгкЦНУц![]() ЃЌФЧУДЦНУц
ЃЌФЧУДЦНУц![]() ФквЛЖЈВЛДцдкжБЯпДЙжБгкЦНУц
ФквЛЖЈВЛДцдкжБЯпДЙжБгкЦНУц![]()
B. ШчЙћЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЦНУц
ЦНУц![]()
C. ВЛДцдкЫФИіНЧЖМЪЧжБНЧЕФПеМфЫФБпаЮ
D. ПеМфЭМаЮОЙ§жааФЭЖгАКѓЃЌжБЯпЛЙЪЧжБЯпЃЌЕЋЦНаажБЯпПЩФмБфГЩЯрНЛЕФжБЯп
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЪЧЪзЯюЮЊa1ЃН![]() ЃЌЙЋБШqЃН
ЃЌЙЋБШqЃН![]() ЕФЕШБШЪ§СаЃЌЩш
ЕФЕШБШЪ§СаЃЌЩш![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ТњзуcnЃНanЁЄbn.
ТњзуcnЃНanЁЄbn.
(1)ЧѓжЄЃК{bn}ЪЧЕШВюЪ§СаЃЛ
(2)ЧѓЪ§Са{cn}ЕФЧАnЯюКЭSnЃЛ
(3)ШєcnЁм![]() m2ЃЋmЃ1ЖдвЛЧае§ећЪ§nКуГЩСЂЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇ.
m2ЃЋmЃ1ЖдвЛЧае§ећЪ§nКуГЩСЂЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЃЌbЃЌcЃЌвбжЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓНЧBЕФДѓаЁЃЛ
ЃЈ2ЃЉШєa+c=1ЃЌЧѓbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгцДЌМзЮЛгкЕКгьAЕФФЯЦЋЮї60ЁуЗНЯђЕФBДІЃЌЧвгыЕКгьAЯрОр12КЃРяЃЌгцДЌвввд10КЃРя/аЁЪБЕФЫйЖШДгЕКгьAГіЗЂбие§ББЗНЯђКНааЃЌШєгцДЌМзЭЌЪБДгBДІГіЗЂбиББЦЋЖЋІСЕФЗНЯђзЗИЯгцДЌввЃЌИеКУгУ2аЁЪБзЗЩЯЃЎ 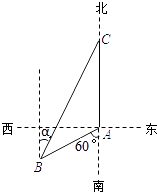
ЃЈ1ЃЉЧѓгцДЌМзЕФЫйЖШЃЛ
ЃЈ2ЃЉЧѓsinІСЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгцДЌМзЮЛгкЕКгьAЕФФЯЦЋЮї60ЁуЗНЯђЕФBДІЃЌЧвгыЕКгьAЯрОр12КЃРяЃЌгцДЌвввд10КЃРя/аЁЪБЕФЫйЖШДгЕКгьAГіЗЂбие§ББЗНЯђКНааЃЌШєгцДЌМзЭЌЪБДгBДІГіЗЂбиББЦЋЖЋІСЕФЗНЯђзЗИЯгцДЌввЃЌИеКУгУ2аЁЪБзЗЩЯЃЎ 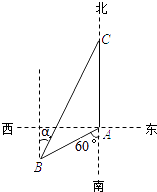
ЃЈ1ЃЉЧѓгцДЌМзЕФЫйЖШЃЛ
ЃЈ2ЃЉЧѓsinІСЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЊЕУЕНКЏЪ§y=cos2xЕФЭМЯѓЃЌжЛашНЋy=cosЃЈ2x+ ![]() ЃЉЕФЭМЯѓЃЈ ЃЉ
ЃЉЕФЭМЯѓЃЈ ЃЉ
A.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШ
ИіЕЅЮЛГЄЖШ
B.ЯђгвЦНвЦ ![]() ИіЕЅЮЛГЄЖШ
ИіЕЅЮЛГЄЖШ
C.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШ
ИіЕЅЮЛГЄЖШ
D.ЯђгвЦНвЦ ![]() ИіЕЅЮЛГЄЖШ
ИіЕЅЮЛГЄЖШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЬжТл![]() ЕФМЋжЕЕуЕФИіЪ§ЃЛ
ЕФМЋжЕЕуЕФИіЪ§ЃЛ
ЃЈЂђЃЉШєЖдгкШЮвт![]() ЃЌзмга
ЃЌзмга![]() ГЩСЂЃЌЧѓЪЕЪ§
ГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВCЕФСНИіНЙЕуЪЧF1ЃЈЉ2ЃЌ0ЃЉЃЌF2ЃЈ2ЃЌ0ЃЉЃЌЧвЭждВCОЙ§ЕуAЃЈ0ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєЙ§ЭждВCЕФзѓНЙЕуF1ЃЈЉ2ЃЌ0ЃЉЧваБТЪЮЊ1ЕФжБЯпlгыЭждВCНЛгкPЁЂQСНЕуЃЌЧѓЯпЖЮPQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com