
 已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),
已知圆锥的底面半径为3,母线长为5,在圆锥内部放置一个内接圆柱(圆柱的一底面与圆锥的底面重合),分析 (Ⅰ)画出圆锥及内接圆柱的轴截面,根据三角形相似对应边成比例,用r表示圆柱的高x,代入圆柱体积公式,可得答案;
(Ⅱ)由(I)中体积的表达式,利用导数法,可得V的最大值点,进而得到V的最大值.
解答 解:(Ⅰ)如下图所示: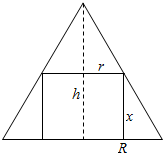
圆锥的底面半径R=3,母线长l=5,
则圆锥的高h=$\sqrt{{5}^{2}-{3}^{2}}$=4,
当圆锥内部放置一个内接圆柱的底面半径为r时,圆柱的高x满足:$\frac{r}{R}=\frac{h-x}{h}$,即x=4-$\frac{4}{3}r$,
故圆柱的体积V=${4{πr}^{2}-\frac{4}{3}πr}^{3}$;
(Ⅱ)由(I)得:V′=8πr-4πr2,
当r∈(0,2)时,V′>0,V随r的增大而增大;
当r∈(2,3)时,V′<0,V随r的增大而减小;
故当r=2时,V取最大值$\frac{16}{3}π$
点评 本题考查的知识点是圆柱和圆锥的几何特征,函数的最大值,难度中档.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
 P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.
P为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}$=1上任意一点,F1,F2为左、右焦点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{2}{3}\sqrt{21}$,$\frac{2}{3}\sqrt{21}$) | B. | (-2,-1)∪(3,4) | C. | (-$\frac{2}{3}\sqrt{21}$,-1) | D. | ($\frac{2}{3}\sqrt{21}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个机器零件的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该机器零件的体积为( )
如图是一个机器零件的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该机器零件的体积为( )| A. | 2+3π+4$\sqrt{2}$ | B. | 2+π | C. | 4+π | D. | 4+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com