已知函数f(x)=x4-2ax2.
(I)求证:方程f(x)=1有实根;
(II)h(x)=f(x)-x在[0,1]上是单调递减的,求实数a的取值范围;
(III)当x∈[0,1]时,关于x的不等式|f′(x)|>1的解集为空集,求所有满足条件的实数a的值.
解:(I)要证x
4-2ax
2=1的实根,
设t=x
2,也就是证明方程t
2-2at=1有非负实数根.
而△=4a
2+4>0,故可设t
2-2at-1=0的两根为t
1,t
2.
t
1t
2=-1,∴t
1,t
2一正一负,
∴方程有正根
∴方程f(x)=1有实根;
(II)由题设知对任意的x∈[0,1]时,
h′(x)=f′(x)-1=4x
3-4ax-1≤0恒成立,
x=0时显然成立;
对任意的0<x≤1,a≥x
2-
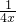
,∴a≥(x
2-
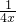
)max
而g(x)=x
2-
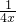
在(0,1]上单调增,
∴a≥f(1)=

,
∴a的取值范围为[

,+∞).
(III)由题设知,当x∈[0,1]时,|4x
3-4ax|≤1恒成立
记F(x)=4x
3-4ax
若a≤0则F(1)=4-4a≥4,不满足条件;
若a>0则F′(x)=12x
2-4a=12(x-

)(x+

)
①当

<1即0<a<3时,F(x)在[0,

]上递减,在[

,1]上递增,
于是,|F(x)|max=max{-F(

),F(1)}=max{
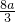

,4-4a}≤1
解之得:a=

②当

≥1即a≥3时,F(x)在[0,1]上递减,于是|F(x)|max=-F(1)=4-4a≥8,与题意矛盾.
综上所述:a=

.
分析:(I)要证x
4-2ax
2=1的实根,设t=x
2,也就是证明方程t
2-2at=1有非负实数根.而△=4a
2+4>0,故可设t
2-2at-1=0的两根为t
1,t
2.利用根与系数的关系即得;
(II)由题设知对任意的x∈[0,1]时,h′(x)=f′(x)-1=4x
3-4ax-1≤0恒成立,对x分类讨论:x=0时显然成立;
对任意的0<x≤1,a≥x
2-
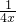
结合函数的单调性即可求出a的取值范围;
(III)由题设知,当x∈[0,1]时,|4x
3-4ax|≤1恒成立,记F(x)=4x
3-4ax,对a分类:若a≤0不满足条件;若a>0则F′(x)=12x
2-4a=12(x-

)(x+

)从而求出满足条件的实数a的值.
点评:本小题主要考查函数单调性的应用、二次函数的性质、一元二次方程的根的分布与系数的关系、不等式的解法等基础知识,考查运算求解能力,考查方程思想、化归与转化思想.属于基础题.

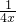 ,∴a≥(x2-
,∴a≥(x2-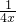 )max
)max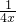 在(0,1]上单调增,
在(0,1]上单调增, ,
, ,+∞).
,+∞). )(x+
)(x+ )
) <1即0<a<3时,F(x)在[0,
<1即0<a<3时,F(x)在[0, ]上递减,在[
]上递减,在[ ,1]上递增,
,1]上递增, ),F(1)}=max{
),F(1)}=max{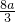
 ,4-4a}≤1
,4-4a}≤1
 ≥1即a≥3时,F(x)在[0,1]上递减,于是|F(x)|max=-F(1)=4-4a≥8,与题意矛盾.
≥1即a≥3时,F(x)在[0,1]上递减,于是|F(x)|max=-F(1)=4-4a≥8,与题意矛盾. .
.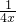 结合函数的单调性即可求出a的取值范围;
结合函数的单调性即可求出a的取值范围; )(x+
)(x+ )从而求出满足条件的实数a的值.
)从而求出满足条件的实数a的值.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<