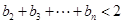(本小题满分14分) 已知数列
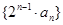
的前n项和S
n=9-6n.
(1)求数列
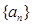
的通项公式.
(2)设
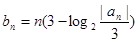
,求数列
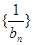
的前n项和.
解:(1)
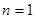
时,
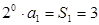
∴
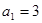
………理1分,文2分
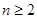
时,
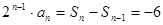
∴
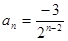
………理3分,文5分
∴通项公式
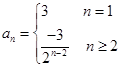
………理5分,文7分
(2)当
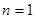
时,
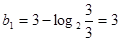
∴
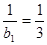
………理6分,文9分
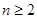
时,
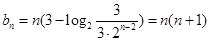
∴
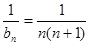
………理7分,文11分
∴
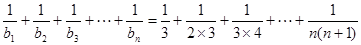
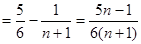
………理9分,文14分
(3)∵

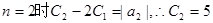
,………理10分
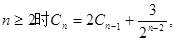
两边同时乘以2
n,得

即
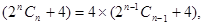
∴数列{
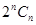
+4}是以6为首项,4为公比的等比数列,
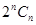
+4 = 6×4
n-1,∴
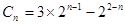
(n≥2) ………理13分
又C
1="1, " 满足上式
∴通项公式
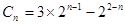
………理14分
法二:(迭代法)
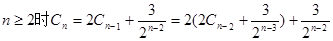
=
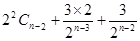
= …… =
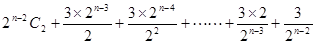
=
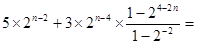
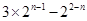
又C
1="1, " 满足上式
∴通项公式
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知等比数列
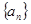
中,
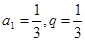
,
(1)
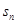
为数列
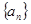
前

项的和,证明:
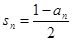
(2)设
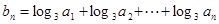
,求数列
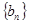
的通项公式;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
本题满分12分)
已知数列
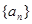
满足
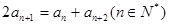
,它的前
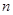
项和为
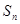
,且
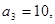
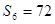
.
①求通项
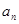
,
②若
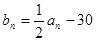
,求数列
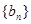
的前
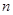
项和的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)数列
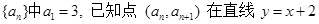
上,
(1)求数列
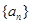
的通项公式; (2)若
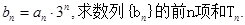
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
… … … …
… … … … …
假设第
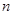
行的第二个数为
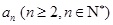
,
(Ⅰ)依次写出第六行的所有
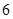
个数字;
(Ⅱ)归纳出
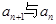
的关系式并求出
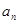
的通项公式;
(Ⅲ)设
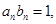
求证:
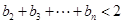
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
( 12分)已知正项数列
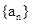
的前n项和满足
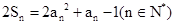
(1)求数列
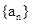
的通项公式;
(2)设
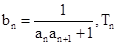
是数列
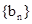
的前n项的和,求证:
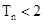
查看答案和解析>>

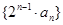 的前n项和Sn=9-6n.
的前n项和Sn=9-6n. 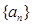 的通项公式.
的通项公式.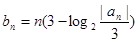 ,求数列
,求数列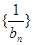 的前n项和.
的前n项和. 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案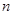 行的第二个数为
行的第二个数为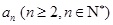 ,
, 个数字;
个数字;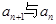 的关系式并求出
的关系式并求出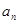 的通项公式;
的通项公式;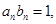 求证:
求证: