
����Ŀ��������������������������Ͷ�����ҹ�����Ѹ�ͷ�չ��������������Ϊ���dz����ṩ�˺ܴ�ı�������Ҳ�����еĹ���������һЩ���ѣ���ij����Ϊ�˽����Ƕ�������������Ͷ�ŵ��Ͽɶȣ���![]() ����ε���Ⱥ�����ȡ
����ε���Ⱥ�����ȡ![]() �˽�����һ�������Ƿ���Ͷ�Ź������������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ�������Ƿ���Ͷ�Ź������������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
��� | ���� | ��Ͷ�ŵ����� | ��Ͷ�ŵ�����ռ�����Ƶ�� |
��һ�� |
|
|
|
�ڶ��� |
|
|
|
������ |
|
|
|
������ |
|
|
|
������ |
|
|
|
������ |
|
|
|
��![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��ֵ��
��ֵ��
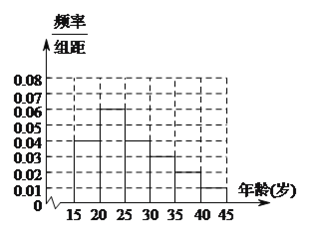
��![]() ���ڵ��ġ��塢��������Ͷ�Ź��������������У��÷ֲ�����ķ�����ȡ
���ڵ��ġ��塢��������Ͷ�Ź��������������У��÷ֲ�����ķ�����ȡ![]() �˲μ��������������ﳵ����������ġ��塢����Ӧ�ֱ��ȡ��������
�˲μ��������������ﳵ����������ġ��塢����Ӧ�ֱ��ȡ��������
��![]() ���ڣ�
���ڣ�![]() ���г�ȡ��
���г�ȡ��![]() �������ѡ��
�������ѡ��![]() ����Ϊ��ӣ�����ѡ�ɵ�
����Ϊ��ӣ�����ѡ�ɵ�![]() ���е�����������һ�˵ĸ��ʣ�
���е�����������һ�˵ĸ��ʣ�
���𰸡�(1) ![]() ��(2)���ġ��塢����ֱ�ȡ������Ϊ
��(2)���ġ��塢����ֱ�ȡ������Ϊ![]() �ˣ�
�ˣ� ![]() �ˣ�
�ˣ� ![]() ����(3)
����(3) ![]() .
.
�����������������(1)��ȫƵ�ʷֲ�ֱ��ͼ����Ƶ�ʱ��е���������ͬ������������Ϊ![]() ���ٽ��Ƶ�ʷֲ�ֱ��ͼ�������
���ٽ��Ƶ�ʷֲ�ֱ��ͼ�������![]() ��ֵ��(2)��Ϊ���ģ��壬����ϲ���ﳵ����������
��ֵ��(2)��Ϊ���ģ��壬����ϲ���ﳵ����������![]() �ˣ����÷ֲ����ԭ����������ģ��壬����ֱ�ȡ��������(3) �������
�ˣ����÷ֲ����ԭ����������ģ��壬����ֱ�ȡ��������(3) �������![]() ��Ϊ��
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��������
��������![]() ����
���� ![]() ��
�� ![]() ��������
��������![]() ����
��Ϊ�� ![]() �������оٷ��������ȡ��
�������оٷ��������ȡ��![]() �������ѡ��
�������ѡ��![]() ����Ϊ��ӣ����������ѡ�ɵ�
����Ϊ��ӣ����������ѡ�ɵ�![]() ���е�����������һ�˵ĸ���.
���е�����������һ�˵ĸ���.
�����������![]() ����ȫƵ�ʷֲ�ֱ��ͼ����ͼ����
����ȫƵ�ʷֲ�ֱ��ͼ����ͼ����
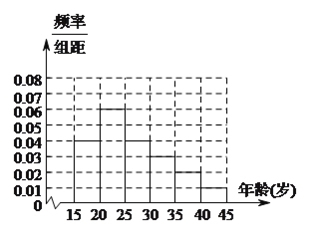
��Ƶ�ʱ��е��������ݿ�֪��������������Ϊ![]() ��
��
�ٽ��Ƶ�ʷֲ�ֱ��ͼ��
��֪![]() ��
��
����![]() ��
��
�ڶ����Ƶ��Ϊ![]() ������
������![]() ��
��
��![]() ����Ϊ���ġ��塢������ϲ���ﳵ������������
����Ϊ���ġ��塢������ϲ���ﳵ������������![]() �ˣ�
�ˣ�
�ɷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ������Ϊ![]() �ˣ�
�ˣ� ![]() �ˣ�
�ˣ� ![]() �ˣ�
�ˣ�
��![]() ���������
���������![]() ����
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
������![]() ����
���� ![]() ��
�� ![]() ��������
��������![]() ����
���� ![]() ��
��
���![]() ���������ȡ
���������ȡ![]() ��������п��ܵĽ��Ϊ��
��������п��ܵĽ��Ϊ��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() �֣�
�֣�
������ѡ�ɵ�![]() ���е�����������һ�˵����п��ܽ��Ϊ��
���е�����������һ�˵����п��ܽ��Ϊ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����11��
����11��
������ѡ�ɵ�![]() ���е�����������һ�˵ĸ���Ϊ
���е�����������һ�˵ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ��
��![]() ����������㣬��
����������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ����
����![]() ʱ��
ʱ�� ![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
��![]() ����
����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��![]() ����
����![]() ������
������![]() �ĵ������䣮
�ĵ������䣮
��![]() ����
����![]() ����
����![]() ������
������![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬʱ�����ھ�Ϊ![]() ��һ�������Ϊ�˶����˵����������������ȣ�����������������и���� 5 ������λ��
��һ�������Ϊ�˶����˵����������������ȣ�����������������и���� 5 ������λ�� ![]() �� ,
�� ,
�ף�25.44��25.43�� 25.41��25.39��25.38
�ң�25.41��25.42�� 25.41��25.39��25.42.
������������ھ��ijߴ翴��˭��������������ϸߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�����![]() �У��ı���
�У��ı���![]() Ϊֱ�����Σ�
Ϊֱ�����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���ı���
���ı���![]() Ϊ����.
����.

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ�ö����
��ʹ�ö����![]() �Ĵ�СΪ
�Ĵ�СΪ![]() �������ڣ�ȷ����
�������ڣ�ȷ����![]() ��λ�ò�����֤��.
��λ�ò�����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ԲO�ǡ�ABC�����Բ��AB=BC��AD��BC���ϵĸߣ�AE��ԲO��ֱ��������C��ԲO�����߽�BA���ӳ����ڵ�F�� 
��1����֤��ACBC=ADAE��
��2����AF=2��CF=2 ![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����[2������1��n]an+[2+����1��n]an+1=1+����1��n��3n����a25��a1= ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com