
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 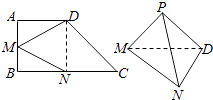
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
【答案】
(1)证明:∵翻折前MB⊥NB,MA⊥DA,∴翻折后MP⊥NP,MP⊥PD,
∵NP∩PD=P,∴MP⊥平面PND,
∵MP平面PMD,∴平面PMD⊥平面PND
(2)解:由题意得AM=BM=PM,BN=CN=PN,AD=CD=PN,
设AM=a,BN=b,作DH⊥BC,NH= ![]() ,
,
∴AD=BN+NH=b+ ![]() ,
,
∴ ![]() =3ab+
=3ab+ ![]() ,
,
S△MND=S梯形ABCD﹣S△AMD﹣S△MBN﹣S△DNC
=3ab+ ![]() ﹣
﹣ ![]()
=ab+ ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() .
.
PO⊥平面MPN,
PO= ![]() =
= ![]() =
= ![]() ,
,
sin ![]() ,
,
如图,  ,
,
解得a= ![]() ,b=
,b= ![]() ,代入上式得sin∠PDO=
,代入上式得sin∠PDO= ![]() .
.
∴直线PD与平面DMN所成角的正弦值为 ![]() .
.

【解析】(1)推导出翻折后MP⊥NP,MP⊥PD,由此能证明平面PMD⊥平面PND.(2)由题意得AM=BM=PM,BN=CN=PN,AD=CD=PN,设AM=a,BN=b,作DH⊥BC,由此入手能求出直线PD与平面DMN所成角的正弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券类稳健型产品的收益与投资额成正比,投资股票类风险型产品的收益与投资额的算术平方根成正比,已知两类产品各投资1万元时的收益分别为0.125万元和0.5万元,如图:
(Ⅰ)分别写出两类产品的收益y(万元)与投资额x(万元)的函数关系;
(Ⅱ)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题: 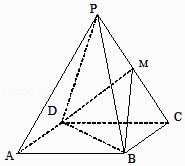
(1)求证:PA∥平面BMD;
(2)求二面角M﹣BD﹣C的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上. (Ⅰ)求异面直线D1E与A1D所成的角;
(Ⅱ)若二面角D1﹣EC﹣D的大小为45°,求点B到平面D1EC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com