
(1)求函数f(x)的最小正周期;
(2)(文)若f(x)的最大值为1,求a的值.
(理)若f(x)在[![]() ,
,![]() ]上最大值与最小值之和为
]上最大值与最小值之和为![]() ,求a的值.
,求a的值.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:044
已知f(x)=sin(x+![]() )+sin(x-
)+sin(x-![]() )+cosx+a(a∈R,a为常数)
)+cosx+a(a∈R,a为常数)
(1)求函数f(x)的最小正周期;
(2)(文)若f(x)的最大值为1,求a的值.
(理)若f(x)在[![]() ,
,![]() ]上最大值与最小值之和为
]上最大值与最小值之和为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省商丘市高三5月第三次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数f(x)=sin(2x-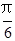 ),则y=f(x)的图象可由函数y=sinx的图象(纵坐标不变)变换如下
),则y=f(x)的图象可由函数y=sinx的图象(纵坐标不变)变换如下
A.先把各点的横坐标伸长到原来的2倍,再向左平移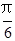 个单位
个单位
B.先把各点的横坐标伸长到原来的2倍,再向右平移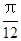 个单位
个单位
C.先把各点的横坐标缩短到原来的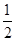 倍,再向左平移
倍,再向左平移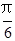 个单位
个单位
D.先把各点的横坐标缩短到原来的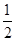 倍,再向右平移
倍,再向右平移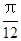 单位
单位
查看答案和解析>>
科目:高中数学 来源:2012届江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)=sinωx(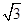 cosωx+sinωx)+
cosωx+sinωx)+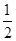 (ω∈R,x∈R)最小正周期为π,且图象关于直线x=
(ω∈R,x∈R)最小正周期为π,且图象关于直线x=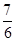 π对称.
π对称.
(1)求f(x)的最大值及对应的x的集合;
(2)若直线y=a与函数y=1-f(x),x∈[0,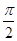 ]的图象有且只有一个公共点,求实数a的范围.
]的图象有且只有一个公共点,求实数a的范围.
查看答案和解析>>
科目:高中数学 来源:广东梅州市曾宪梓中学2010-2011学年高三10月考数学文 题型:选择题
已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为 ( )
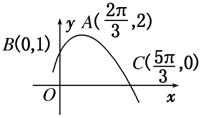 A.f(x)=2sin(+)
A.f(x)=2sin(+)
B.f(x)=sin(4x+)
C.f(x)=2sin(-)
D.f(x)=sin(4x-)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com