练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．某小朋友按如下规则练习数数，1大拇指，2食指，3中指，4无名指，5小指，6无名指，7中指，8食指，9大拇指，10食指，…一直数到2016时，对应的指头是（　　）
    A．小指B．中指C．食指D．大拇指

    分析 根据所给的数据：发现大拇指对的数是1+8n，小指对的数是5+8n，其中n∈Z，食指、中指、无名指对的数介于它们之间．因2013=251×8+5，数到2013时对应的指头是小指．因此可知数到2016时对应的指头是食指．

    解答 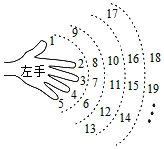解：∵大拇指对的数是1+8n，小指对的数是5+8n，其中n∈Z，
    又∵2013=251×8+5，
    ∴数到2013时对应的指头是小指．
    故知数到2016时对应的指头是食指．
    故选：C．

    点评 此题是个中档题．考查学生观察、归纳和分析解决问题的能力．只需找出大拇指和小指对应的数的规律即可．关键规律为：大拇指对的数是1+8n，小指对的数是5+8n，其中n∈Z．食指、中指、无名指对的数介于它们之间．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．$\root{3}{（-6）^{3}}$+$\root{4}{（\sqrt{5}-4）^{4}}$+$\root{3}{（\sqrt{5}-4）^{3}}$的值为-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数$f（x）=lnx-\frac{1}{4}x+\frac{3}{4x}-1$，g（x）=x2-2bx+4，若对任意x1∈（0，2），存在x2∈[1，2]，使f（x1）≥g（x2），则实数b的取值范围是[$\frac{17}{8}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=$\frac{{x}^{2}-3}{{e}^{x}}$在区间（0，a）上单调，则a的最大值是3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．观察下列等式1=12，12-22=-3，12-22+32=6，12-22+32-42=-10照此规律，第100个等式12-22+32-42+…-1002=-5050．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

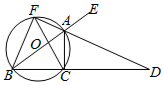    11．如图，已知四边形ACBF内接于圆O，FA，BC的延长线交于点D，且FB=FC，AB是△ABC的外接圆的直径．
    （1）求证：AD平分∠EAC；
    （2）若AD=4$\sqrt{3}$，∠EAC=120°，求BC的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．[$\sqrt{n}$]表示不超过$\sqrt{n}$的最大整数．若
    S1=[$\sqrt{1}$]+[$\sqrt{2}$]+[$\sqrt{3}$]=3，
    S2=[$\sqrt{4}$]+[$\sqrt{5}$]+[$\sqrt{6}$]+[$\sqrt{7}$]+[$\sqrt{8}$]=10，
    S3=[$\sqrt{9}$]+[$\sqrt{10}$]+[$\sqrt{11}$]+[$\sqrt{12}$]+[$\sqrt{13}$]+[$\sqrt{14}$]+[$\sqrt{15}$]=21，
    …，
    则Sn=（　　）
    A．n（n+2）B．n（n+3）C．（n+1）2-1D．n（2n+1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知2sinα+cosα=0，求下列各式的值：
    （1）$\frac{2cosα-sinα}{sinα+cosα}$          
    （2）$\frac{sinα}{si{n}^{3}α-co{s}^{3}α}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．将点的直角坐标（-2，2$\sqrt{3}$）化为极坐标为（　　）
    A．（4，$\frac{2}{3}$π）B．（-4，$\frac{2}{3}$π）C．（-4，$\frac{1}{3}$π）D．（4，$\frac{1}{3}$π）

    查看答案和解析>>

    同步练习册答案