
【题目】设f(x)是定义在R上且周期为1的函数,在区间[0,1)上,f(x)= ![]() ,其中集合D={x|x=
,其中集合D={x|x= ![]() ,n∈N*},则方程f(x)﹣lgx=0的解的个数是 .
,n∈N*},则方程f(x)﹣lgx=0的解的个数是 .
【答案】8
【解析】解:∵在区间[0,1)上,f(x)= ![]() ,
,
第一段函数上的点的横纵坐标均为有理数,
又f(x)是定义在R上且周期为1的函数,
∴在区间[1,2)上,f(x)= ![]() ,此时f(x)的图象与y=lgx有且只有一个交点;
,此时f(x)的图象与y=lgx有且只有一个交点;
同理:
区间[2,3)上,f(x)的图象与y=lgx有且只有一个交点;
区间[3,4)上,f(x)的图象与y=lgx有且只有一个交点;
区间[4,5)上,f(x)的图象与y=lgx有且只有一个交点;
区间[5,6)上,f(x)的图象与y=lgx有且只有一个交点;
区间[6,7)上,f(x)的图象与y=lgx有且只有一个交点;
区间[7,8)上,f(x)的图象与y=lgx有且只有一个交点;
区间[8,9)上,f(x)的图象与y=lgx有且只有一个交点;
在区间[9,+∞)上,f(x)的图象与y=lgx无交点;
故f(x)的图象与y=lgx有8个交点;
即方程f(x)﹣lgx=0的解的个数是8,
所以答案是:8


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣ ![]() <x<
<x< ![]() ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.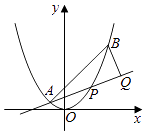
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excosx﹣x.(13分)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年1月,北京经历了59年来雾霾天气最多的一个月.据气象局统计,北京市2013年1月1日至1月30日这30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》如表1:
表1 空气质量指数AQI分组表
AQI指数M | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
表2是某气象观测点记录的连续4天里AQI指数M与当天的空气水平可见度y(km)的情况,表3是某气象观测点记录的北京市2013年1月1日至1月30日的AQI指数频数分布表.
表2 AQI指数M与当天的空气水平可见度y(km)的情况
AQI指数M | 900 | 700 | 300 | 100 |
空气水平可见度y(km) | 0.5 | 3.5 | 6.5 | 9.5 |
表3 北京市2013年1月1日至1月30日AQI指数频数分布表
AQI指数M | [0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x=![]() ,根据表2的数据,求出y关于x的线性回归方程.
,根据表2的数据,求出y关于x的线性回归方程.
(参考公式: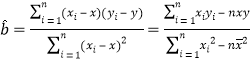 ,
,![]() .)
.)
(2)小王在北京开了一家洗车店,经小王统计:当AQI指数低于200时,洗车店平均每天亏损约2000元;当AQI指数在200至400时,洗车店平均每天收入约4000元;当AQI指数不低于400时,洗车店平均每天收入约7000元.
①估计小王的洗车店在2013年1月份平均每天的收入;
②从AQI指数在[0,200)和[800,1000]内的这6天中抽取2天,求这2天的收入之和不低于5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(Ⅰ)求b关于a的函数关系式,并写出定义域;
(Ⅱ)证明:b2>3a;
(Ⅲ)若f(x),f′(x)这两个函数的所有极值之和不小于﹣ ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C: ![]() +y2=1上,过M做x轴的垂线,垂足为N,点P满足
+y2=1上,过M做x轴的垂线,垂足为N,点P满足 ![]() =
= ![]() .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点Q在直线x=﹣3上,且 ![]()
![]() =1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
=1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为5的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
求:(1)求圆的方程;
(2)设直线![]() 与圆相交于
与圆相交于![]() 两点,求实数
两点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?
?
若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com