
【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.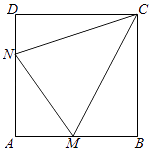
【答案】解:(Ⅰ)当点M,N分别是边AB,AD的中点时,设∠DCN=∠BCM=θ, CD=BC=1,DN=BM= ![]() ,CN=CM=
,CN=CM= ![]() ,sinθ=
,sinθ= ![]() ,cosθ=
,cosθ= ![]() ,∠MCN=
,∠MCN= ![]() ﹣2θ,
﹣2θ,
所以cos∠MCN=cos( ![]() ﹣2θ)=sin2θ=2sinθcosθ=
﹣2θ)=sin2θ=2sinθcosθ= ![]() ,
,
所以∠MCN的余弦值是 ![]() .
.
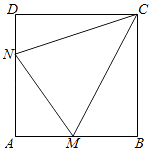
(Ⅱ)设∠BCM=α,∠DCN=β,AM=x,AN=y,则BM=1﹣x,DN=1﹣y,
在△CBM中,tanα=1﹣x,在△CDN中,tanβ=1﹣y,
所以:tan(α+β)= ![]() =
= ![]() =
= ![]() ,(*)
,(*)
△AMN的周长为2千米,所以x+y+ ![]() =2,化简得xy=2(x+y)﹣2,
=2,化简得xy=2(x+y)﹣2,
代入(*)式,可得tan(α+β)= ![]() =
= 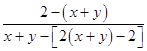 =
= ![]() =1,
=1,
所以α+β= ![]() ,所以∠MCN是定值,且∠MCN=
,所以∠MCN是定值,且∠MCN= ![]() .
. 
【解析】(Ⅰ)设∠DCN=∠BCM=θ,由题意利用勾股定理可求CN=CM= ![]() ,从而可求sinθ=
,从而可求sinθ= ![]() ,cosθ=
,cosθ= ![]() ,∠MCN=
,∠MCN= ![]() ﹣2θ,利用诱导公式,二倍角公式即可求∠MCN的余弦值.(Ⅱ)设∠BCM=α,∠DCN=β,AM=x,AN=y,可求BM=1﹣x,DN=1﹣y,tanα=1﹣x,tanβ=1﹣y,可得tan(α+β)=
﹣2θ,利用诱导公式,二倍角公式即可求∠MCN的余弦值.(Ⅱ)设∠BCM=α,∠DCN=β,AM=x,AN=y,可求BM=1﹣x,DN=1﹣y,tanα=1﹣x,tanβ=1﹣y,可得tan(α+β)= ![]() ,由x+y+
,由x+y+ ![]() =2,化简得xy=2(x+y)﹣2,求得tan(α+β)=1,即可得解∠MCN是定值,且∠MCN=
=2,化简得xy=2(x+y)﹣2,求得tan(α+β)=1,即可得解∠MCN是定值,且∠MCN= ![]() .
.
【考点精析】利用两角和与差的正切公式对题目进行判断即可得到答案,需要熟知两角和与差的正切公式:![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=1,E,F分别是CC1 , BC的中点.
(Ⅰ)求证:B1F⊥平面AEF;
(Ⅱ)求三棱锥E﹣AB1F的体积.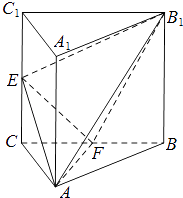
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)是否存在实数![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅱ)在 (Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个说法:
①若函数f(x)=asinx+cosx(x∈R)的图象关于直线x= ![]() 对称,则a=
对称,则a= ![]() ;
;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),若
=(﹣2,m),若 ![]() 与
与 ![]() 的夹角为钝角,则m<1;
的夹角为钝角,则m<1;
③当 ![]() <α<
<α< ![]() 时,函数f(x)=sinx﹣logax有三个零点;
时,函数f(x)=sinx﹣logax有三个零点;
④函数f(x)=xsinx在[﹣ ![]() ,0]上单调递减,在[0,
,0]上单调递减,在[0, ![]() ]上单调递增.
]上单调递增.
其中正确的是(填上所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 (其中
(其中![]() ,
, ![]() ).
).
(Ⅰ)当![]() 时,若
时,若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() 的图象在两点
的图象在两点![]() 、
、![]() 处的切线分别为
处的切线分别为![]() 、
、![]() ,若
,若![]() ,
, ![]() ,且
,且![]() ,求实数
,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀的骰子先后抛掷两次,若第一次朝上一面的点数为a,第二次朝上一面的点数为b,则函数y=ax2﹣2bx+1在(﹣∞,2]上为减函数的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
序号 | 分组 | 组中值 | 频数 | 频率 |
1 | [60,70) | 65 | ① | 0.10 |
2 | [70,80) | 75 | 20 | ② |
3 | [80,90) | 85 | ③ | 0.20 |
4 | [90,100) | 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
(1)求出频率分布表中①、②、③、④、⑤的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生获奖?
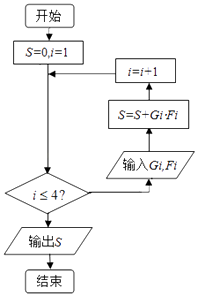
(3)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序的功能是什么?求输出的S的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 
A.30°
B.60°
C.45°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com